# 写在前面

最近又看了大牛Jian-Feng Cai[1]的系列文章，先占一个坑[2]，这个与以前的Cadzow算法有关系，以后慢慢补充大牛的其他文章。

# 符号介绍

考虑下面一维信号含噪模型

y=s+e\boldsymbol y = \boldsymbol s +\boldsymbol e

Cadzow去噪法基于干净信号s\boldsymbol s的Hankel矩阵低秩性质进行截断奇异值分解。首先对复信号z\boldsymbol z进行Hankel化（Hankelization）

Hz=[z0z1z2⋯zK−1z1z2z3⋯zKz2z3z4⋯zK+1⋮⋮⋮⋮⋮zL−1zLzL+1⋯zN−1]\mathcal H \boldsymbol z = \begin{bmatrix} z_0 & z_1 & z_2 & \cdots & z_{K-1}\\ z_1 & z_2 & z_3 & \cdots & z_{K}\\ z_2 & z_3 & z_4 & \cdots & z_{K+1}\\ \vdots & \vdots & \vdots & \vdots & \vdots\\ z_{L-1} & z_{L} & z_{L+1} & \cdots & z_{N-1} \end{bmatrix}

其逆过程记为H†\mathcal H^\dagger，对给定矩阵Z∈CL×KZ\in\mathbb C^{L\times K}进行反对角平均。记第aa个反对角线上元素个数为

wa=#{(i,j)∣i+j=a,0≤i≤L−1,0≤j≤K−1}w_a = \#\left\{ (i,j)~|~ i+j=a,~ 0\leq i\leq L-1,~0\leq j\leq K-1\right\}

去Hanekl化得到的向量H†Z\mathcal H^\dagger Z的第aa个元素为

[H†Z]a=1wa∑i+j=a[Z]ij[\mathcal H^\dagger Z]_a=\frac{1}{w_a} \sum_{i+j=a}[Z]_{ij}

注意： H†H=I\mathcal H^\dagger\mathcal H=\mathcal I为恒等映射，而PMH=HH†\mathcal P_{\mathcal M_{\mathcal H}} = \mathcal H\mathcal H^\dagger为矩阵到Hankel矩阵空间MH\mathcal M_{\mathcal H}的投影。

# Cadzow算法

前面提到Cadzow去噪的核心思想，假设rank(Hx)=r≪min⁡(L,K)\text{rank}(\mathcal H\boldsymbol x)=r \ll\min{(L,K)}，而rank(Hy)=min⁡(L,K)\text{rank}(\mathcal H\boldsymbol y)=\min{(L,K)}。因此从y\boldsymbol y到x\boldsymbol x需要进行降秩。令z0=y\boldsymbol z_0 = \boldsymbol y，通过如下迭代

zk+1=H†TrHzk,k=0,⋯\boldsymbol z_{k+1} = \mathcal H^\dagger\mathcal T_r\mathcal H\boldsymbol z_k,~k=0,\cdots

其中Tr\mathcal T_r为奇异值分解Z=∑j=1min⁡(L,K)σjujvj∗Z=\sum_{j=1}^{\min(L,K)}\sigma_j\boldsymbol{u}_j\boldsymbol{v}_j^*的截断形式，记秩rr矩阵集合为Mr\mathcal M_r

Tr(Z)=∑j=1rσjujvj∗∈Mr\mathcal{T}_r(Z)=\sum_{j=1}^r\sigma_j\boldsymbol{u}_j\boldsymbol{v}_j^*\in\mathcal M_r

截断奇异值分解过程可视为矩阵到Mr\mathcal M_r的投影，记为PMr\mathcal P_{\mathcal M_r}。

值得注意的是，Cadzow算法是多通道奇异谱分析，且Cadzow算法的第一次迭代与奇异谱分析完全一致。此外，Cadzow算法与交替投影相关。令Zk=HzkZ_k = \mathcal H\boldsymbol z_k，Cadzow算法的矩阵表示形式如下

Zk+1=PMHPMrZk,k=0,⋯Z_{k+1} = \mathcal P_{\mathcal M_H}\mathcal P_{\mathcal M_r}Z_k,~k=0,\cdots

当观测信号存在缺省值时，能否通过部分信号恢复完整信号？Cadzow算法的一种变体可很好地进行信号恢复。令z0=PΩ(x)\boldsymbol z_0=\mathcal P_\Omega(\boldsymbol x)迭代如下过程

zk+1=PΩ(x)+(I−PΩ)H†TrHzk,k=0,⋯\boldsymbol z_{k+1} = \mathcal P_\Omega(\boldsymbol x)+(\mathcal I-\mathcal P_\Omega)\mathcal H^\dagger\mathcal T_r\mathcal H\boldsymbol z_k,~k=0,\cdots

其中第二项H†TrHzk\mathcal H^\dagger\mathcal T_r\mathcal H\boldsymbol z_k用来更新Ωc\Omega^c的未知分量。如果观测信号被高斯噪声扰动，则可以把第一项改为PΩ(H†TrHzk)\mathcal P_\Omega(\mathcal H^\dagger\mathcal T_r\mathcal H\boldsymbol z_k)来消除噪声的影响。

# 快速Cadzow算法

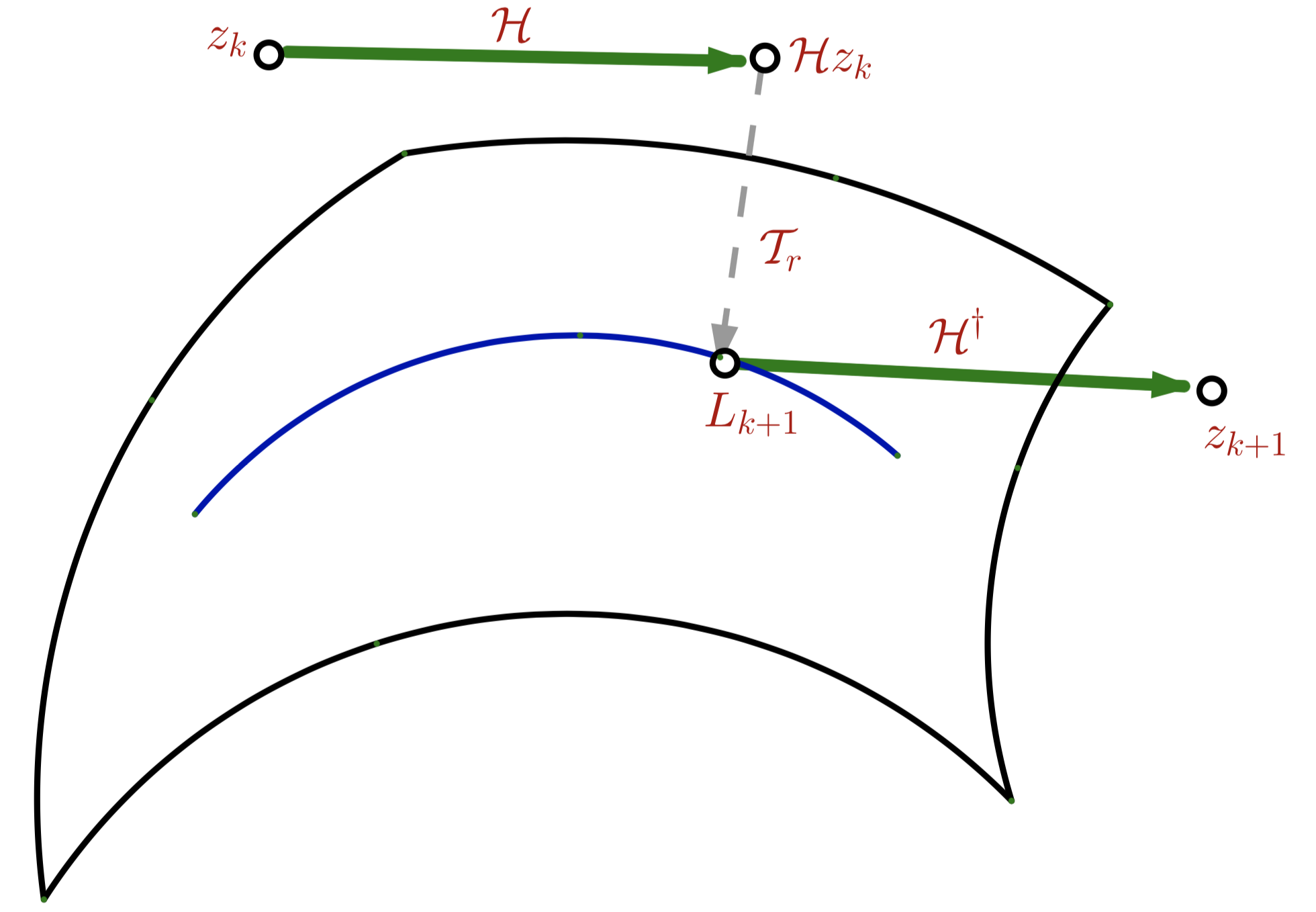
# Cadzow算法图解

zk+1=H†TrHzk,k=0,⋯\boldsymbol z_{k+1} = \mathcal H^\dagger\mathcal T_r\mathcal H\boldsymbol z_k,~k=0,\cdots

该算法里的Hankel化H\mathcal H和逆Hankel化H†\mathcal H^\dagger是向量与矩阵间的转化，而奇异值分解则是对Hankel矩阵进行操作。从图中可以看见，投影是在对应集合中找到距离最近的点，对应点是投影点。

对于信号z∈Cn\boldsymbol z\in\mathbb C^{n}，矩阵Hz∈CL×K\mathcal H\boldsymbol z\in\mathbb C^{L\times K}的奇异值分解计算复杂度在O(N3)\mathcal O(N^3)。为了加快收敛速度，可以在Hzk\mathcal H\boldsymbol z_k做一些改动，使得进行投影PMr\mathcal P_{\mathcal M_r}时效率更高。那么最直接的方法就是改变矩阵的结构，在特定的子空间进行奇异值分解，利用代数的方法来降低整体迭代的计算复杂度。

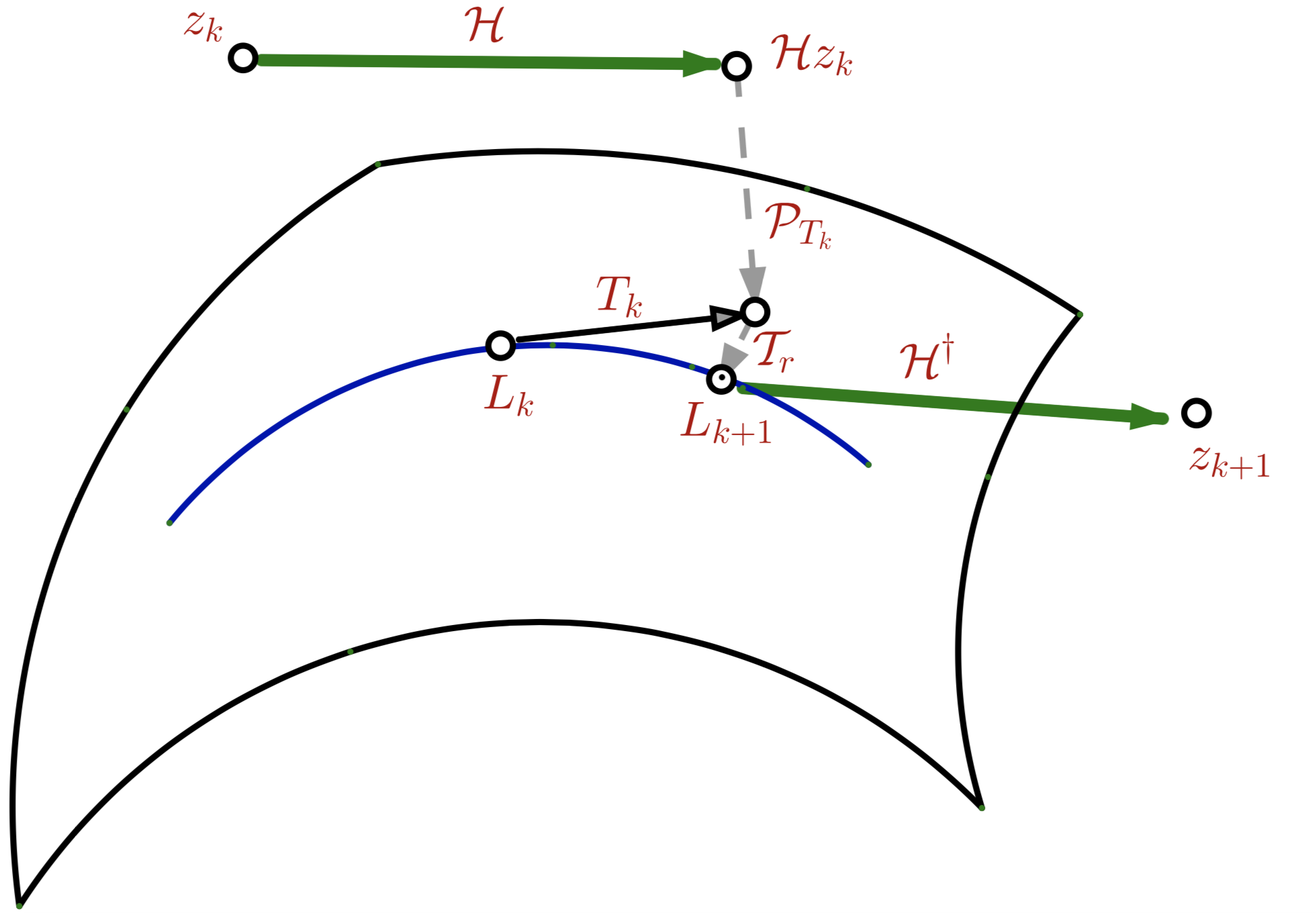
# 快速Cadzow算法图解

zk+1=H†TrPTkHzk\boldsymbol z_{k+1}=\mathcal H^\dagger\mathcal T_r\mathcal P_{T_k}\mathcal H\boldsymbol z_k

与Cadzow算法相比，快速在于多加了到子空间Tk∈CL×KT_k\in\mathbb C^{L\times K}一个投影PTk\mathcal P_{T_k}，选择合适的子空间可以赋予PTkHzk\mathcal P_{T_k}\mathcal H\boldsymbol z_k利于分解的矩阵结构。

# TkT_k的选择

前一个迭代点zk=H†TrPTk−1Hzk−1\boldsymbol z_{k}=\mathcal H^\dagger\mathcal T_r\mathcal P_{T_{k-1}}\mathcal H\boldsymbol z_{k-1}的秩rr部分记为Lk=TrPTk−1Hzk−1L_k = \mathcal T_r\mathcal P_{T_{k-1}}\mathcal H\boldsymbol z_{k-1}，则LkL_k的简化奇异值分解为Lk=UkΣVk∗L_k=U_k\Sigma V_k^*，则TkT_k可通过LkL_k的行、列子空间的直和来构造

Tk={UkB∗+CVk∗∣B∈CK×r,C∈CL×r}T_k = \{U_kB^*+CV_k^*~|~B\in\mathbb C^{K\times r},~C\in\mathbb C^{L\times r}\}

秩rr矩阵形成一个光滑流形，而TkT_k是流形上点LkL_k处的切空间。有了子空间TkT_k后，任意点Z∈CL×KZ\in\mathbb C^{L\times K}到TkT_k的投影为

PTk(Z)=UkUk∗Z+ZVkVk∗−UkUk∗ZVkVk∗.\mathcal P_{T_k}(Z) = U_kU_k^*Z+ZV_kV_k^*-U_kU_k^*ZV_kV_k^*.

  • 第一次迭代设置T0∈CL×KT_0\in\mathbb C^{L\times K}，也就是说快速Cadzow算法与Cadzow算法第一步是一致的。
  • 第k+1k+1次迭代点的投影子空间TkT_k都是依赖第kk次迭代点由奇异值分解得到正交子空间直和，这也解释了快速Cadzow算法图上的TkT_k为LkL_k的切空间。
  • 当LkL_k具有近似Hankel矩阵结构时，HH†Lk≈Lk\mathcal H\mathcal H^\dagger L_k\approx L_k且Lk∈TkL_k\in T_k，有PTkHzk≈Hzk\mathcal P_{T_k}\mathcal H\boldsymbol z_k\approx \mathcal H\boldsymbol z_k，由此Hzk\mathcal H\boldsymbol z_k到TkT_k的投影能捕获其最大的能量。

# 算法复杂度

与矩阵TrHzk∈CL×K\mathcal T_r\mathcal H\boldsymbol z_k\in\mathbb C^{L\times K}的奇异值分解相比，通过到TkT_k的投影，矩阵TrPTk−1Hzk−1\mathcal T_r\mathcal P_{T_{k-1}}\mathcal H\boldsymbol z_{k-1}可化成2r×2r2r\times 2r的奇异值分解。将快速Cadzow算法分解为三步：

{Wk=PTkHzkLk+1=TrWkzk+1=H†Lk+1.\begin{cases} W_k = \mathcal P_{T_k}\mathcal H\boldsymbol z_k\\ L_{k+1} = \mathcal T_r W_k\\ \boldsymbol z_{k+1} =\mathcal H^\dagger L_{k+1}. \end{cases}

令Hk=HzkH_k=\mathcal H\boldsymbol z_k，得到到TkT_k的投影点

Wk=UkUk∗Hk+HkVkVk∗−UkUk∗HkVkVk∗=UkUk∗HkVkVk∗+UkUk∗Hk(I−VkVk∗)+(I−UkUk∗)HkVkVk∗=UkGVk∗+UkB∗+CVk∗\begin{aligned} W_k&=U_kU_k^*H_k+H_kV_kV_k^*-U_kU_k^*H_kV_kV_k^*\\ &=U_kU_k^*H_kV_kV_k^*+U_kU_k^*H_k(I-V_kV_k^*)+(I-U_kU_k^*)H_kV_kV_k^*\\ &=U_kGV_k^* + U_kB^*+CV_k^* \end{aligned}

其中

G=Uk∗HkVkB=(I−VkVk∗)Hk∗UkC=(I−UkUk∗)HkVk\begin{aligned} G&=U_k^*H_kV_k\\ B&=(I-V_kV_k^*)H_k^*U_k\\ C&=(I-U_kU_k^*)H_kV_k \end{aligned}

对BB和CC进行QR分解

B=(I−VkVk∗)Hk∗Uk=Q1R1C=(I−UkUk∗)HkVk=Q2R2\begin{aligned} B&=(I-V_kV_k^*)H_k^*U_k=Q_1R_1\\ C&=(I-U_kU_k^*)H_kV_k=Q_2R_2 \end{aligned}

则Q1⊥Vk,Q2⊥UkQ_1\perp V_k,\quad Q_2\perp U_k，且

Wk=UkGVk∗+UkR1∗Q1∗+Q2R2Vk∗=[UkQ2][GR1∗R20][VkQ1]∗=([UkQ2]UG)ΣG([VkQ1]VG)∗\begin{aligned} W_k& = U_kGV_k^* + U_kR_1^*Q_1^*+Q_2R_2V_k^*\\ &=\begin{bmatrix}U_k & Q_2\end{bmatrix} \begin{bmatrix} G& R_1^*\\ R_2 & \boldsymbol {0} \end{bmatrix} \begin{bmatrix} V_k&Q_1 \end{bmatrix}^*\\ &=\left(\begin{bmatrix}U_k & Q_2\end{bmatrix}U_G\right)\Sigma_G\left(\begin{bmatrix} V_k&Q_1 \end{bmatrix}V_G\right)^* \end{aligned}

其中涉及一个2r×2r2r\times 2r矩阵的奇异值分解

[GR1∗R20]=UGΣGVG∗.\begin{bmatrix} G& R_1^*\\ R_2 & \boldsymbol {0} \end{bmatrix} = {U}_G\Sigma_G{V}_G^*.

因此总的计算复杂度为O(Nr2+Nrlog⁡N+r3)\mathcal O(Nr^2+Nr\log N+r^3)，空间复杂度为O(Nr)\mathcal O(Nr)。

# 算法流程图

# 梯度方向

将Cadzow算法重新表示为

Zk+1=PMHPMrZk=PMHPMr(Zk+t(Y−Zk)),t=0,\begin{aligned} Z_{k+1} &= \mathcal P_{\mathcal M_H}\mathcal P_{\mathcal M_r}Z_k\\ &=\mathcal P_{\mathcal M_H}\mathcal P_{\mathcal M_r}(Z_k+t(Y-Z_k)),\quad t=0, \end{aligned}

其中Zk=HzkZ_k=\mathcal H\boldsymbol z_k和Y=Hy=H(x+e)Y = \mathcal H\boldsymbol y=\mathcal H(\boldsymbol x+\boldsymbol e)，则Cadzow算法可表示为一类投影梯度方法，其对应的优化问题为

min⁡12∥Z−Y∥F2 s.t rank(Z)≤r and Z is Hankel\min\frac{1}{2}\|Z-Y\|_F^2 ~\text{s.t}~ \text{rank}(Z)\leq r \text{ and }Z\text{ is Hankel}

由于Hankel矩阵端点效应，考虑如下重加权优化问题

min⁡12∥W⊙(Z−Y)∥F2 s.t rank(Z)≤r and Z is Hankel\min\frac{1}{2}\|\sqrt{W}\odot(Z-Y)\|_F^2 ~\text{s.t}~ \text{rank}(Z)\leq r \text{ and }Z\text{ is Hankel}

其中权值矩阵WW为

W=H(w0,⋯,wN−1)=[11213⋮⋮1213⋮⋮⋮13⋮⋮⋮13⋮⋮⋮1312⋮⋮13121].\begin{aligned} \sqrt{W}&=\mathcal H(\sqrt{w_0},\cdots,\sqrt{w_{N-1}})\\ &= \begin{bmatrix} 1 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} & \vdots & \vdots\\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}}& \vdots & \vdots & \vdots\\ \frac{1}{\sqrt{3}} & \vdots & \vdots & \vdots &\frac{1}{\sqrt{3}}\\ \vdots & \vdots & \vdots & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{2}}\\ \vdots & \vdots & \frac{1}{\sqrt{3}} &\frac{1}{\sqrt{2}}& 1 \end{bmatrix}. \end{aligned}

令步长为1，则投影梯度法表示为

Zk+1=PMHPMr(Zk+W⊙(Y−Zk)).Z_{k+1} = \mathcal P_{\mathcal M_H}\mathcal P_{\mathcal M_r}(Z_k+W\odot(Y-Z_k)).

记1/D=[1/w0,⋯,1/wN−1]⊤1/D = [1/w_0,\cdots,1/w_{N-1}]^\top，Cadzow算法对应的梯度算法如下

若引入投影子空间，则可得到快速Cadzow算法对应的快速梯度算法。

# 小结

下面会继续看一些低秩Hankel矩阵相关的文章。

# References

  1. Jian-Feng Cai Homepage: http://www.math.ust.hk/~jfcai/ (opens new window) ↩︎

  2. H. Wang, J.-F. Cai, T. Wang, and K. Wei, Fast Cadzow's Algorithm and a Gradient Variant, arxiv preprint: 1906.03572. ↩︎

基于黎曼几何的多分类算法