# 写在前面

以前看算法时，Majorization-Minimization算法经常出现，借助一些blog[1]和slide[2],^,[3],^,[4],^,[5],^,[6]来总结下。

# MM算法是什么

MM算法是优化领域的一个重要方法。与其说它是一个具体算法，不如说是一个算法框架，因为很多具体的算法都可以被推断成MM算法，例如坐标下降法(coordinate descent)、近端梯度法(proximal gradient)、EM算法等等。

回到MM算法。复杂的优化问题不方便直接处理时，通常期望找到一个近似的问题或者近似的解来间接解决原问题。再看算法名字

Majorization+Minimization\text{Majorization}+\text{Minimization}

当然，该算法也存在反面

Minorization+Maximization\text{Minorization}+\text{Maximization}

显然意味着两个步骤交替进行

  • 找到一个可以控制迭代点趋于最优解的优化函数
  • 求解该近似函数为目标的最优化

从数学角度来说，MM算法的核心思想是连续上限最小化(Successive upper bound minimization)，设计一系列近似的优化(majorizing)函数来控制原函数的上限，通过最小化序列来收敛至原目标的最优解。

简单来说，MM算法将原始的优化问题转化为一系列简单的优化问题，让求解变得更简单。

# 优化函数定义

目标函数f(x)f(x)在点xkx_k处的优化函数g(x∣xk)g(x|x_k)满足两点性质

  • 占优条件(dominance condition)

    g(x∣xk)≥f(x),∀xg(x | x_k) \ge f(x), \quad \forall x

  • 切线条件(tangent condition)

    g(xk∣xk)=f(xk),∀xkg(x_k | x_k) = f(x_k), \quad \forall x_k

即g(x∣xk)g(x|x_k)在f(x)f(x)上方且相切于点x=xkx= x_k。

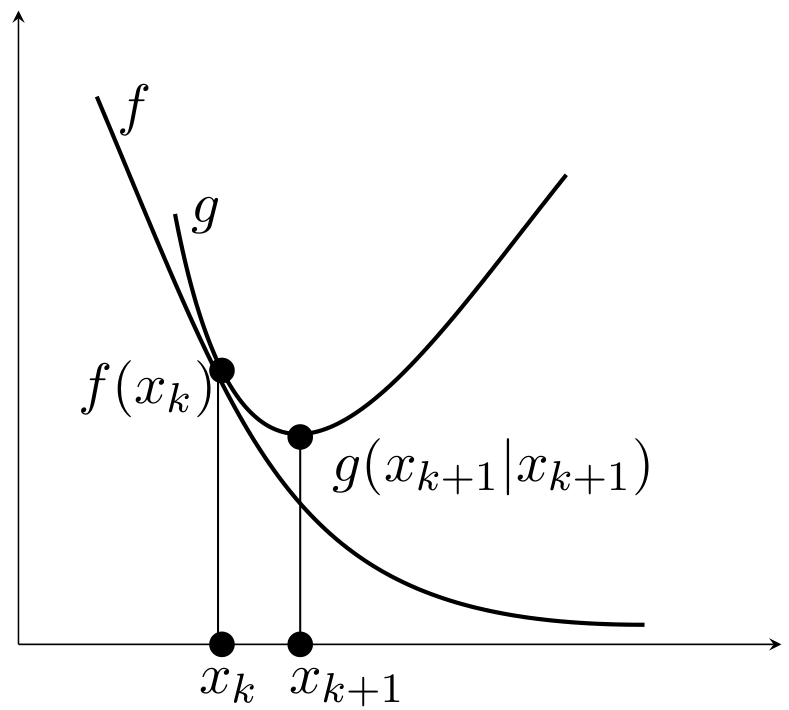
只要满足这两个条件，如下迭代产生的序列必能收敛至局部最优解。

xk+1=arg⁡min⁡xg(x∣xk)x_{k+1} = \arg\min_x g(x|x_k)

这是因为

f(xk+1)≤g(xk+1∣xk)≤g(xk∣xk)=f(xk)f(x_{k+1}) \leq g(x_{k+1}|x_k) \leq g(x_k|x_k) = f(x_k)

注意：

  • MM算法得到的序列保证目标函数值非增
  • 更新的序列点用于构造下一代的优化函数
  • 优化函数通常用于分裂参数(split parameters)，从而可以逐元素进行更新。

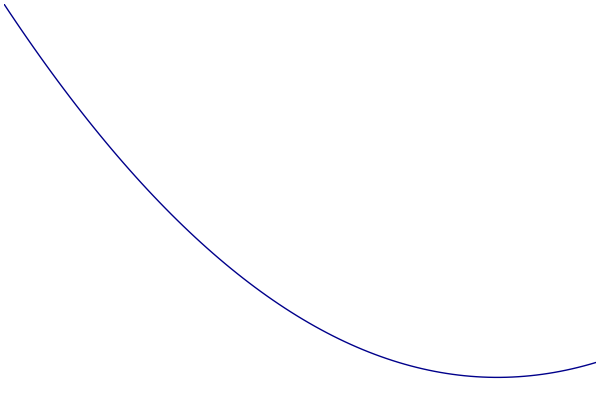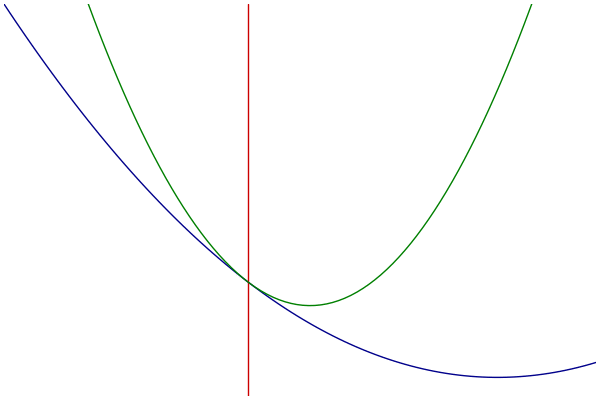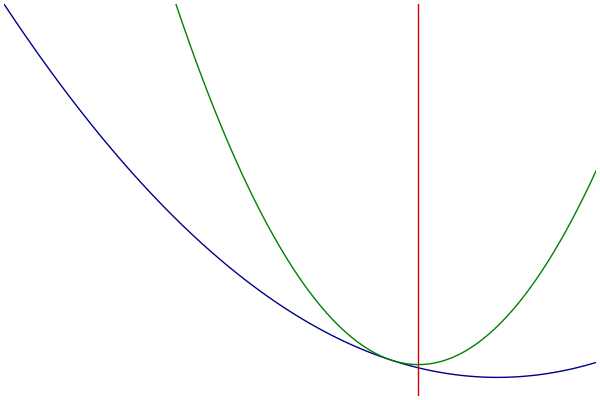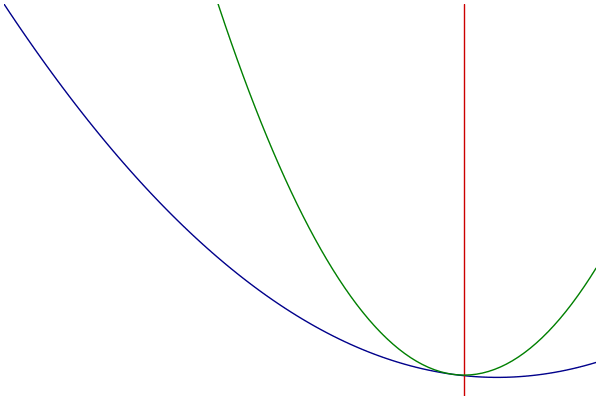
# MM过程可视化

  • 蓝色：原始的目标函数
  • 绿色：一系列优化函数
  • 红色：切点的选择

# 优化函数的构造

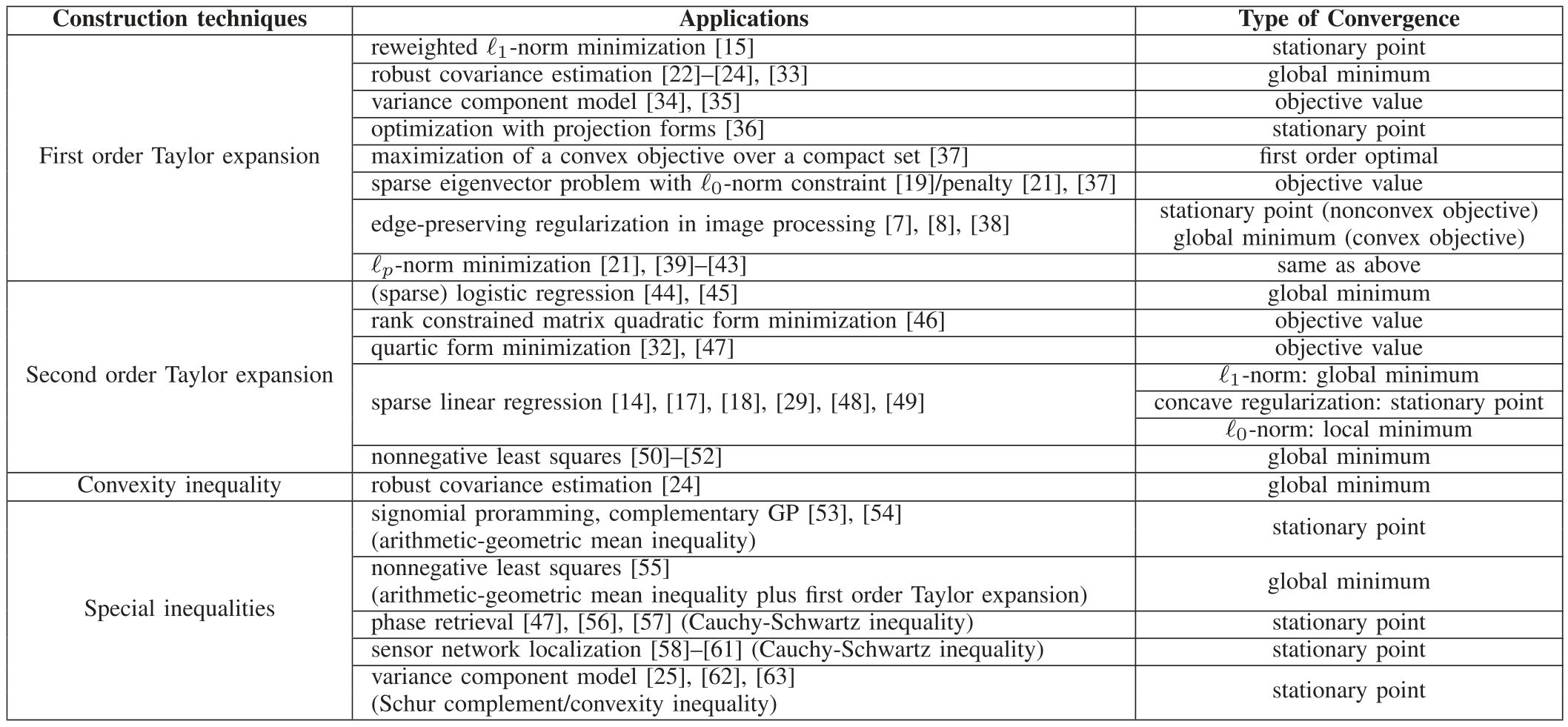
选择合适的优化函数尤为重要，通常有四种方式[7]：一阶泰勒展开、二阶泰勒展开、凸性不等式和特殊不等式。

# 一阶泰勒展开

一阶可微函数ff在点x0x_0处的泰勒展开为

f(x)=f(x0)+∇fT(x0)(x−x0)+Of(x)=f\left(x_{0}\right)+\nabla f^{T}\left(x_{0}\right)\left(x-x_{0}\right)+\mathcal O

  • 若ff为凹函数，一阶泰勒展开是ff的全局向下估计(underestimator)，对应于Minorization Maximization，即

    f(x)≥f(x0)+∇fT(x0)(x−x0)f(x) \geq f\left(x_{0}\right)+\nabla f^{T}\left(x_{0}\right)\left(x-x_{0}\right)

  • 若ff为凸函数，一阶泰勒展开是ff的全局向上估计(overestimator)，对应于Majorization Minimization，即

    f(x)≤f(x0)+∇fT(x0)(x−x0)f(x) \leq f\left(x_{0}\right)+\nabla f^{T}\left(x_{0}\right)\left(x-x_{0}\right)

# 二阶泰勒展开

若函数ff是二阶可微的，在点xkx_k处的泰勒展开为

f(x)=f(xk)+∇fT(xk)(x−xk)+12(x−xk)T∇2f(ξ)(x−xk)+O\begin{aligned} f(x)=&f\left(x_{k}\right)+\nabla f^{T}\left(x_{k}\right)\left(x-x_{k}\right)\\ &+\frac{1}{2}\left(x-x_{k}\right)^{T} \nabla^{2} f(\xi)\left(x-x_{k}\right)+\mathcal O \end{aligned}

对应的优化函数可设置为二次函数

g(x∣xk)=f(xk)+∇fT(xk)(x−xk)+12(x−xk)TM(x−xk)\begin{aligned} g(x|x_k) =& f\left(x_{k}\right)+\nabla f^{T}\left(x_{k}\right)\left(x-x_{k}\right) \\ &+\frac{1}{2}\left(x-x_{k}\right)^{T} M \left(x-x_{k}\right) \end{aligned}

其中M⪰∇2f(x),∀xM \succeq \nabla^{2} f(x),\forall x，即M−∇2f(x)M - \nabla^{2} f(x)为半正定矩阵，则有

g(x∣xk)−f(x)=12(x−xk)T(M−∇2f(ξ))(x−xk)≥0g(x|x_k) - f\left(x\right) = \frac{1}{2}\left(x-x_{k}\right)^{T} \left(M - \nabla^{2} f(\xi)\right) \left(x-x_{k}\right) \geq 0

说明gg控制了ff。MM的选择不唯一，通常选M=∇2f(x)+δIM = \nabla^{2} f(x) + \delta I。

选择二阶泰勒展开作为优化函数g(x∣xk)g(x|x_k)后，迭代更新存在闭形式

xk+1=xk−M−1∇f(xk).x_{k+1} = x_k - M^{-1}\nabla f(x_k).

可以理解为二次函数求极小点，而更新公式类似于Newton法，但使用了保证目标函数下降的Hessian矩阵的近似。

# 应用

# 最小二乘

考虑一个最小二乘问题

f(x)=∥Ax−b∥22f(x) = \|Ax-b\|_2^2

其一阶导和二阶导计算如下：

∇f(x)=2AT(Ax−b)∇2f(x)=2ATA\begin{aligned} \nabla f(x) &= 2A^T(Ax-b) \\ \nabla^{2} f(x) &= 2A^TA \end{aligned}

因此ff在点xkx_k处的二阶泰勒展开式为

f(x)=f(xk)+2AT(Axk−b)(x−xk)+2(x−xk)TATA(x−xk)\begin{aligned} f(x) = &f(x_k) + 2A^T(Ax_k-b)(x-x_k)\\ & + 2(x-x_k)^TA^TA(x-x_k) \end{aligned}

构造优化函数

g(x∣xk)=f(xk)+2AT(Axk−b)(x−xk)+2(x−xk)TM(x−xk)\begin{aligned} g(x|x_k) = &f(x_k) + 2A^T(Ax_k-b)(x-x_k)\\ & + 2(x-x_k)^TM(x-x_k) \end{aligned}

其中仅需要对角阵满足M⪰ATAM\succeq A^TA，可以取M=ATA+δIM = A^TA + \delta I，其中δ>0\delta > 0。

# 非负矩阵分解

给定向量xx，非负矩阵分解模型如下

f(W,h)=∥Wh−x∥22f(W,h) = \|Wh-x\|_2^2

同样做二阶泰勒展开

f(W,h)=f(hk)+2WT(Whk−x)(h−hk)+2(h−hk)TWTW(h−hk)\begin{aligned} f(W,h) =& f(h_k) + 2W^T(Wh_k-x)(h-h_k) \\ &+ 2(h-h_k)^TW^TW(h-h_k) \end{aligned}

取对角矩阵M=diag([WTWh]i[h]i)M = \text{diag}(\frac{[W^TWh]_i}{[h]_i})，则有M⪰WTWM\succeq W^TW，对应的优化函数为

g(W,h∣hk)=f(hk)+2WT(Whk−x)(h−hk)+2(h−hk)TM(h−hk)\begin{aligned} g(W,h|h_k) =& f(h_k) + 2W^T(Wh_k-x)(h-h_k) \\ &+ 2(h-h_k)^TM(h-h_k) \end{aligned}

# Logistic回归

利用样本xix_i以及二元响应变量yi∈{0,1}y_i\in\{0, 1\}，训练回归模型如下：

f(β)=∑i{−yixiTβ+ln⁡[1+exp⁡(xiTβ)]}f(\beta) = \sum_i \left\{-y_i x_i^T\beta + \ln\left[1 + \exp(x_i^T\beta)\right]\right\}

其一阶导和二阶导计算如下：

∇f(β)=∑i−[yi−yi^(β)]xi∇2f(β)=∑iyi^(β)[1−yi^(β)]xixiT\begin{aligned} \nabla f(\beta) &= \sum_i -[y_i - \hat{y_i}(\beta)]x_i \\ \nabla^{2} f(\beta) &= \sum_i \hat{y_i}(\beta)[1 - \hat{y_i}(\beta)]x_i x_i^T \end{aligned}

设y^i(β)=(1+exp⁡(−xiTβ))−1\hat{y}_i(\beta) = (1 + \exp(-x_i^T\beta))^{-1}，下面构造优化函数：

  • Hessian矩阵形式为∇2f(β)=XTWX\nabla^{2} f(\beta) = X^TWX，其中对角矩阵WW的对角元素为y^i(1−y^i)\hat{y}_i(1 - \hat{y}_i)
  • y^i∈(0,1)\hat{y}_i\in (0,1)，所以14≥y^i(1−y^i)\frac{1}{4} \ge \hat{y}_i(1 - \hat{y}_i)
  • 选择M=XTX/4M = X^TX/4则可构造二次上限(quadratic upper bound)

更新规则如下

  • MM算法

    β(t+1)=β(t)−4(XTX)−1XT(y−y^(β(t)))\beta^{(t+1)} = \beta^{(t)} - 4\left(X^TX\right)^{-1}X^T(y - \hat{y}(\beta^{(t)}))

    整个过程只需要计算一次矩阵的逆(XTX)−1(X^TX)^{-1}

  • Newton算法

    β(t+1)=β(t)−(XTWX)−1XT(y−y^(β(t)))\beta^{(t+1)} = \beta^{(t)} - \left(X^TWX\right)^{-1}X^T(y - \hat{y}(\beta^{(t)}))

    每次迭代需反复计算矩阵的逆(XTWX)−1\left(X^TWX\right)^{-1}

这个例子不难发现，目标函数ff是光滑的凸函数，所以只需要找到函数二阶导的上界，就能利用二阶泰勒展开式，很容易构造出一系列优化函数，此外优化函数的最小化存在闭解，为原问题减少了大量的计算成本。

# DC programming

假设函数ff可表示两个可微的凸函数之差，即

f(x)=g(x)−h(x)f(x) = g(x) - h(x)

通常认为ff是非凸的，因此传统的凸分析算法不再适用，但是该函数可分解为凸函数(gg)与凹函数(−h-h)之和，因此不妨对后者进行一阶展开得到线性函数(既是凸函数又是凹函数)

u(x∣xk)=g(x)−(h(xk)+∇hT(xk)(x−xk))u(x|x_k) = g(x) - \left(h(x_k)+\nabla h^{T}\left(x_{k}\right)\left(x-x_{k}\right)\right)

不难看出

  • u(x∣xk)≥f(x),∀xu(x|x_k) \geq f(x), \quad \forall x

  • u(xk∣xk)=f(xk)u(x_k|x_k) = f(x_k)

则线性化后的表示u(x∣xk)u(x|x_k)可作为优化函数来控制原函数f(x)f(x)。

# ℓ2−ℓp\ell_2 - \ell_p优化问题

考虑如下常见的优化问题(p≥1p\geq 1)

f(x)=12∥Ax−y∥22+μ∥x∥pf(x) = \frac{1}{2} \|Ax-y\|_2^2 + \mu\|x\|_p

  • 当矩阵AA为单位阵或酉阵时，最优解存在闭解形式

    x∗=ATy−ProjC(ATy)x^* = A^Ty - \text{Proj}_C(A^Ty)

    • C={x:∥x∥p∗≤μ}C=\{x:\|x\|_{p^*} \leq \mu\}
    • ∥⋅∥p∗\|\cdot\|_{p^*}是∥⋅∥p\|\cdot\|_{p}的对偶范数
    • ProjC\text{Proj}_C是投影算子
    • 当p=1p=1时，最优解可用软阈值算子(soft-thresholding)表示

  • 对于更一般形式的矩阵AA，不存在闭解形式的最优解，下面就用MM算法来给出迭代步骤。

关键在于构造优化函数，首先定义如下距离函数

dist(x∣xk)=c2∥x−xk∥22−12∥Ax−Axk∥22\text{dist}(x|x_k) = \frac{c}{2}\|x-x_k\|_2^2 - \frac{1}{2}\|Ax-Ax_k\|_2^2

其中参数cc满足c>λmax⁡(ATA)c>\lambda_{\max}(A^TA)。显然有

  • dist(x∣xk)≥0,∀x\text{dist}(x|x_k) \geq 0,\forall x

  • dist(xk∣xk)=0\text{dist}(x_k|x_k) = 0

将dist(x∣xk)\text{dist}(x|x_k)加到原函数上则可作为优化函数来控制原函数f(x)f(x)。

g(x∣xk)=f(x)+dist(x∣xk)=c2∥x−xˉk∥22+μ∥x∥p+const\begin{aligned} g(x|x_k) &= f(x) + \text{dist}(x|x_k)\\ &= \frac{c}{2}\|x-\bar x_k\|_2^2 + \mu \|x\|_p + \text{const} \end{aligned}

其中

xˉk=1cAT(y−Axk)+xk\bar x_k = \frac{1}{c}A^T(y-Ax_k) + x_k

另外，原函数ff不存在显式的最优解，而优化函数g(x∣xk)g(x|x_k)存在显式的最优解(退化到矩阵AA为单位阵这一特殊情形)。

# 期望最大化（EM）算法

给定一个随机观察变量ww，用对数似然函数最小化来估计θ\theta

θ^ML=arg⁡min⁡θ−ln⁡p(w∣θ)\hat \theta _{\text{ML}} = \arg\min_\theta -\ln p(w|\theta)

  • E-step

    g(θ,θr)=Ez∣w,θr{ln⁡p(w,z∣θ)}g(\theta,\theta^r) = \mathbb E_{z|w,\theta^r}\{\ln p(w,z|\theta)\}

  • M-step

    θr+1=arg⁡min⁡θg(θ,θr)\theta^{r+1} = \arg\min_\theta g(\theta,\theta^r)

迭代产生一个{−ln⁡p(w∣θr)}\{-\ln p(w|\theta^r)\}的非减序列。

对目标函数运用Jensen不等式可得到优化函数

−ln⁡p(w∣θ)=−ln⁡Ez∣θp(w∣z,θ)=−ln⁡Ez∣θ[p(z∣w,θr)p(w∣z,θ)p(z∣w,θr)]=−ln⁡Ez∣w,θr[p(z∣θ)p(w∣z,θ)p(z∣w,θr)](interchange integrations)≤−Ez∣w,θrln⁡[p(z∣θ)p(w∣z,θ)p(z∣w,θr)](Jensen’s inequality)=−Ez∣w,θrln⁡p(w,z∣θ)+Ez∣w,θrln⁡p(z∣w,θr)≜u(θ,θr)\begin{aligned} &\begin{aligned} &-\ln p(w \mid \theta) \\ =&-\ln \mathbb{E}_{z \mid \theta} p(w \mid z, \theta) \\ =&-\ln \mathbb{E}_{z \mid \theta}\left[\frac{p\left(z \mid w, \theta^{r}\right) p(w \mid z, \theta)}{p\left(z \mid w, \theta^{r}\right)}\right] \end{aligned}\\ &=-\ln \mathbb{E}_{z \mid w, \theta^{r}}\left[\frac{p(z \mid \theta) p(w \mid z, \theta)}{p\left(z \mid w, \theta^{r}\right)}\right] (\text{interchange integrations})\\ &\leq-\mathbb{E}_{z \mid w, \theta^{r}} \ln \left[\frac{p(z \mid \theta) p(w \mid z, \theta)}{p\left(z \mid w, \theta^{r}\right)}\right] (\text{Jensen's inequality})\\ &\begin{array}{l} =-\mathbb{E}_{z \mid w, \theta^{r}} \ln p(w, z \mid \theta)+\mathbb{E}_{z \mid w, \theta^{r}} \ln p\left(z \mid w, \theta^{r}\right) \\ \triangleq u\left(\theta, \theta^{r}\right) \end{array} \end{aligned}

  • u(θ,θr)u\left(\theta, \theta^{r}\right)是−ln⁡p(w∣θ)-\ln p(w|\theta)的优化函数

    • u(θ,θr)≥−ln⁡p(w∣θ),∀θu\left(\theta, \theta^{r}\right) \geq -\ln p(w|\theta), \forall \theta

    • u(θr,θr)=−ln⁡p(w∣θr)u\left(\theta^{r}, \theta^{r}\right) = -\ln p(w|\theta^{r})

  • EM算法与MM算法的联系

    • u(θ,θr)u(\theta, \theta^{r})与θ\theta有关的只有第一项
    • E-step本质上是构建u(θ,θr)u(\theta, \theta^{r})，等价于构建g(θ,θr)g(\theta, \theta^{r})
    • M-step最小化u(θ,θr)u(\theta, \theta^{r})，等价于最小化g(θ,θr)g(\theta, \theta^{r})

# 优势 or 原理

体现在

  • 避免矩阵求逆
  • 分离问题的参数（并行计算）
  • 使优化问题线性化（DC programming）
  • 优雅地处理平等和不平等的约束
  • 恢复对称性
  • 将一个非平滑问题变成一个平滑问题
  • 优化函数优化的闭解

迭代计算则是需要付出的代价。

# 参考文献

  1. https://seqstat.com/blog/2016-12-24-mm-algorithms/ (opens new window) ↩︎

  2. Majorization-Minimization Algorithm (opens new window) ↩︎

  3. Majorization Minimization - the Technique of Surrogate (opens new window) ↩︎

  4. Majorization Minimization (MM) and Block Coordinate Descent (BCD) (opens new window) ↩︎

  5. Examples of MM Algorithms (opens new window) ↩︎

  6. Generalized Majorization-Minimization (opens new window) ↩︎

  7. Y. Sun, P. Babu and D. P. Palomar. Majorization-Minimization Algorithms in Signal Processing, Communications, and Machine Learning, IEEE Transactions on Signal Processing, vol. 65, no. 3, pp. 794-816, 1 Feb.1, 2017. ↩︎

结构化低秩近似