# 写在前面

介绍一篇基于任务驱动下的字典学习[1]，本文还参照了一个挺有意思的slide[2]。

# 数据驱动字典学习

数据驱动字典学习强调的是数据自适应性，其目标是获取观测信号的字典实现最佳逼近的稀疏编码表示。假设训练集为X=[x1,…,xn]\mathbf X=[\mathbf x_1,\ldots,\mathbf x_n]，经验损失函数为

gn(D)≜1n∑i=1nℓu(x,D)g_n (\mathbf D)\triangleq \frac{1}{n}\sum_{i=1}^n \ell_u (\mathbf x,\mathbf D)

其下标ℓu\ell_u表示无监督学习方式(unsupervised)。ℓu(x,D)\ell_u (\mathbf x,\mathbf D)作为稀疏编码问题的最优值，可选用如下的elastic-net形式：

ℓu(x,D)≜min⁡α∈Rp12∥x−Dα∥22+λ1∥α∥1+λ22∥α∥22\ell_u (\mathbf x,\mathbf D) \triangleq \min_{\boldsymbol\alpha \in \mathbb R^p} \frac{1}{2}\|\mathbf x-\mathbf D\boldsymbol\alpha\|_2^2 + \lambda_1 \|\boldsymbol\alpha\|_1 + \frac{\lambda_2}{2}\|\boldsymbol\alpha\|_2^2

  • 当λ2=0\lambda_2=0，ℓu(x,D)\ell_u (\mathbf x,\mathbf D)导出ℓ1\ell_1稀疏分解问题，见基追踪(basis pursuit)、Lasso等相关论文。

  • 为避免字典原子出现ℓ2\ell_2范式任意大的问题，通常限制字典如下约束

    D≜{D∈Rm×ps.t.∀j∈{1,…,p},∥dj∥2≤1}\mathcal D \triangleq \{\mathbf D \in \mathbb R^{m \times p} \text{s.t.} \forall j \in \{1,\ldots,p\},\|\mathbf d_j\|_2 \leq 1 \}

  • 经验损失到期望损失：

    Ex[ℓu(x,D)]=a.s.lim⁡n→∞gn(D)\mathbb E_{\mathbf x}[\ell_u (\mathbf x,\mathbf D)] \stackrel{\text{a.s.}}{=}\lim_{n \to \infty} g_n(\mathbf D)

# 稀疏表示

稀疏表示是采用基函数对原始数据进行编码，可以简单地理解为线性表示。

稀疏表示则采用冗余的基函数，而主成分分析采用正交基来重构数据，所以主成分分析的系数并非稀疏。

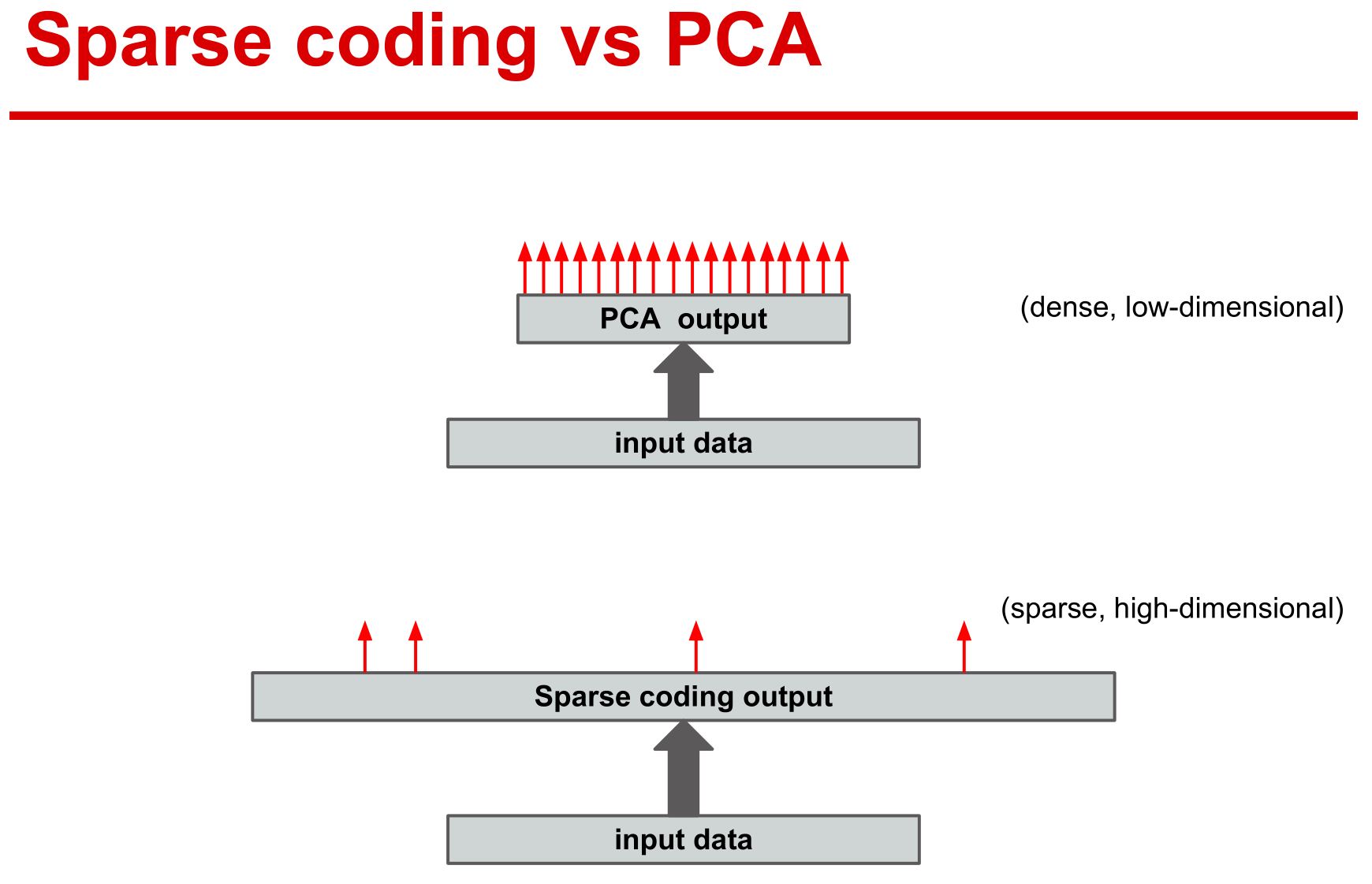
# 字典学习

字典学习需要同时求解字典和稀疏编码，优化对两个变量而言是非凸的。

但是对单个变量是凸的，所以采用交替迭代的方式进行变量更新。

# 监督学习方式

# 基本形式

记elastic-net的稀疏解为

α⋆(x,D)≜arg min⁡α∈Rp12∥x−Dα∥22+λ1∥α∥1+λ22∥α∥22\boldsymbol\alpha^\star(\mathbf x,\mathbf D)\triangleq \operatorname*{arg\,min}_{\boldsymbol\alpha \in \mathbb R^p} \frac{1}{2}\|\mathbf x-\mathbf D\boldsymbol\alpha\|_2^2 + \lambda_1 \|\boldsymbol\alpha\|_1 + \frac{\lambda_2}{2}\|\boldsymbol\alpha\|_2^2

下面使用稀疏向量α⋆(x,D)\boldsymbol\alpha^\star(\mathbf x,\mathbf D)作为信号x\mathbf x的特征来估计对应的标签y\mathbf y，一般都是最小化期望风险

min⁡W∈Wf(W)+ν2∥W∥F2\min_{\mathbf W\in\mathcal W} f(\mathbf W) + \frac{\nu}{2}\|\mathbf W\|_F^2

其中W\mathbf W是需要学习的模型参数。凸函数ff定义如下：

f(W)≜Ey,x[ℓs(y,W,α⋆(x,D))]f(\mathbf W) \triangleq \mathbb E_{\mathbf y,\mathbf x}[\ell_s (\mathbf y,\mathbf W,\boldsymbol\alpha^\star(\mathbf x,\mathbf D))]

与ℓu\ell_u不同，在给定模型参数W\mathbf W和α⋆(x,D)\boldsymbol\alpha^\star(\mathbf x,\mathbf D)稀疏特征下，ℓs\ell_s度量了预测标签与真实标签的接近程度，所以ℓs\ell_s是以监督学习(supervised)的方式选择不同的损失函数，例如二次函数、logistic函数或hinge函数等。注意，到目前为止，所用的字典都是无监督学习ℓu(x,D)\ell_u (\mathbf x,\mathbf D)最优化得到的，但用来重构的字典D\mathbf D并不适用于监督学习任务，这就有了如下监督学习的方式

min⁡D∈D,W∈Wf(D,W)+ν2∥W∥F2\min_{\mathbf D\in\mathcal D,\mathbf W\in\mathcal W} f(\mathbf D,\mathbf W) + \frac{\nu}{2}\|\mathbf W\|_F^2

其中f(D,W)f(\mathbf D,\mathbf W)则需要同时学习参数W\mathbf W和字典D\mathbf D。

f(D,W)≜Ey,x[ℓs(y,W,α⋆(x,D))]f(\mathbf D,\mathbf W) \triangleq \mathbb E_{\mathbf y,\mathbf x}[\ell_s (\mathbf y,\mathbf W,\boldsymbol\alpha^\star(\mathbf x,\mathbf D))]

  • 引入字典变量D\mathbf D后，α⋆\boldsymbol\alpha^\star的不可微分不利于优化问题的求解。
  • 常规做法是引入稀疏正则化的光滑近似项。

监督与非监督的区别在于字典的过完备性：

  • 非监督是衡量预测样本与真实样本的误差，需要冗余的稀疏表示
  • 监督则衡量预测标签与真实标签的差异，仅需要获取具有鉴别的特征，严格的过完备不再需要。

传统的监督学习先获取数据表示，再挖掘特征，这是一种典型的多步骤式的机器学习方式，每一步最优的并不代表整体工程最优。

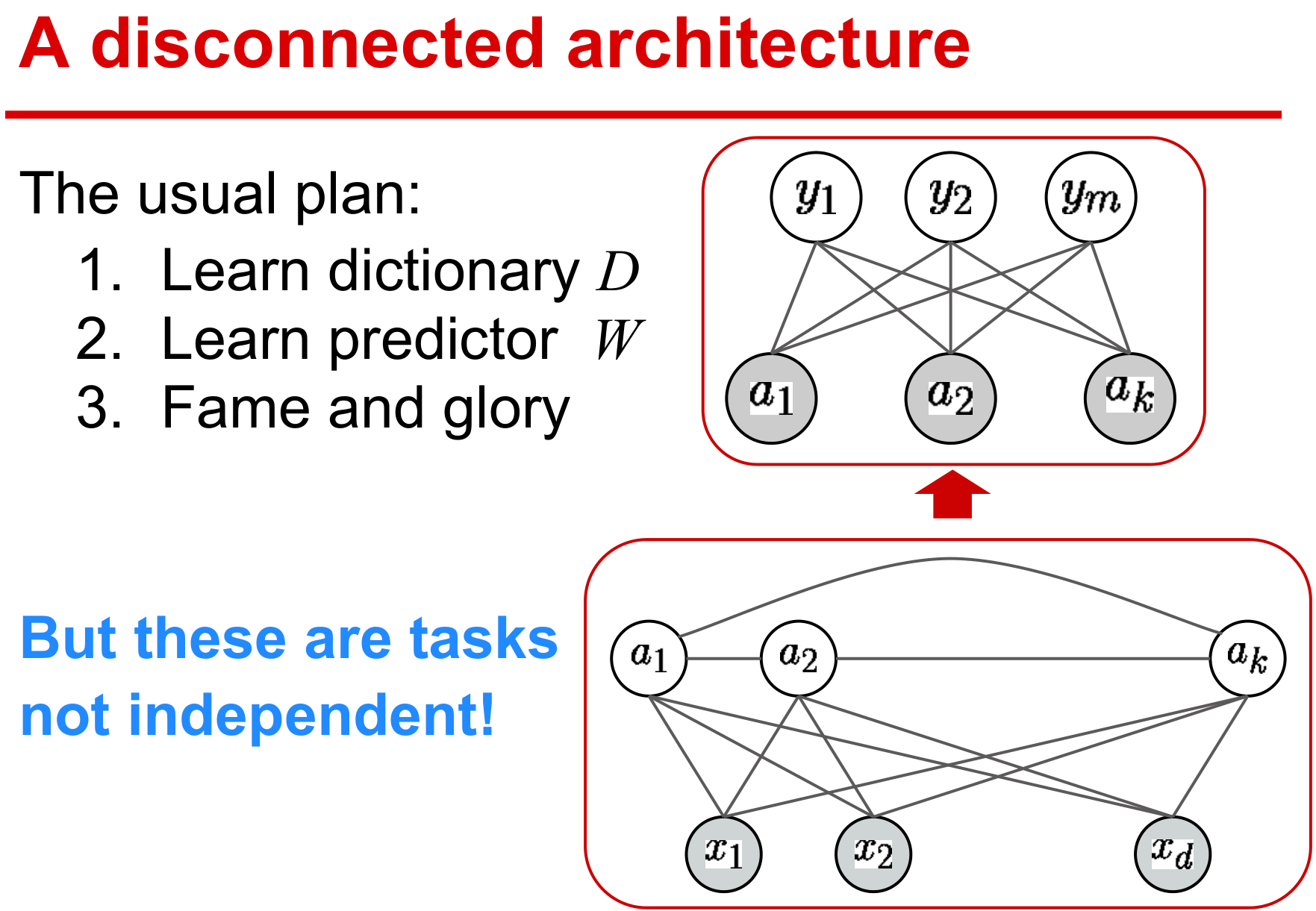
目前方法都期望设计端到端的学习方式，在统一的结构下学习有效参数，保证整体性能最优。

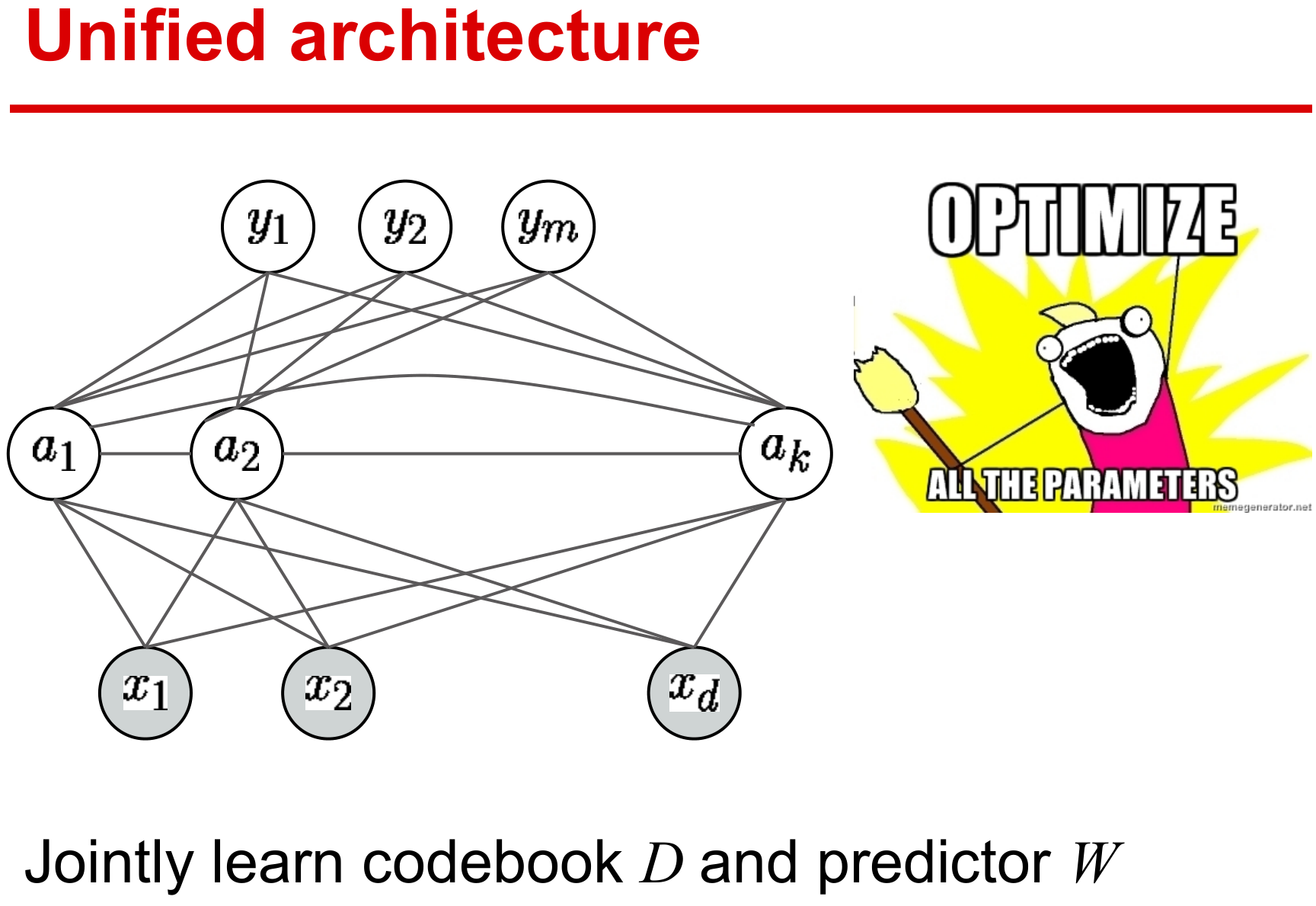
# 基本假设

  • (y,x)(\mathbf y,\mathbf x)服从概率密度函数pp，其紧支撑集KY×KX⊆Y×XK_{\mathcal Y} \times K_{\mathcal X} \subseteq \mathcal Y \times \mathcal X。
  • 当Y\mathcal Y为有限维实向量空间的子集时，pp为连续且ℓs\ell_s二次连续可微。
  • 当Y\mathcal Y为有限的标签集合时，p(y,⋅)p(\mathbf y,\cdot)为连续且ℓs(y,⋅)\ell_s(\mathbf y,\cdot)二次连续可微。

# 输入数据的线性变换

在监督学习基本形式上，考虑增加一个线性变换Z\mathbf Z得到如下模型

min⁡D∈D,W∈W,Z∈Zf(D,W,Z)+ν12∥W∥F2+ν22∥Z∥F2\min_{\mathbf D \in \mathcal D, \mathbf W \in \mathcal W, \mathbf Z \in \mathcal Z} f(\mathbf D,\mathbf W,\mathbf Z) +\frac{\nu_1}{2}\|\mathbf W\|_F^2 + \frac{\nu_2}{2}\|\mathbf Z\|_F^2

其中f(D,W,Z)f(\mathbf D,\mathbf W,\mathbf Z)则需要同时学习参数W\mathbf W、字典D\mathbf D和线性变换Z\mathbf Z。

f(D,W,Z)≜Ey,x[ℓs(y,W,α⋆(Zx,D))]f(\mathbf D,\mathbf W,\mathbf Z) \triangleq \mathbb E_{\mathbf y,\mathbf x}[\ell_s (\mathbf y,\mathbf W,\boldsymbol\alpha^\star(\mathbf Z\mathbf x,\mathbf D))]

该线性变换Z\mathbf Z具有如下作用：

  • 通过线性变换可降低特征空间的维度
  • 通过增加模型的参数使得模型表现能力更强

# 半监督学习

稀疏编码技术可有效地从无标签数据中学习到好的特征，因此下面给出一个监督和无监督相结合的半监督模型。

min⁡D∈D,W∈W(1−μ)Ey,x[ℓs(y,W,α⋆(x,D))]+μEx[ℓu(x,D)]+ν2∥W∥F2\min_{\mathbf D \in \mathcal D, \mathbf W \in \mathcal W} (1-\mu)\mathbb E_{\mathbf y,\mathbf x} [\ell_s\big(\mathbf y,\mathbf W, \boldsymbol\alpha^\star (\mathbf x,\mathbf D)\big)] + \mu \mathbb E_{\mathbf x} [\ell_u(\mathbf x,\mathbf D)] + \frac{\nu}{2}\|\mathbf W\|_F^2

# 任务驱动字典学习

下面将前面的基本优化模型应用至多种任务上，例如回归、分类、压缩感知。分类可视为回归的特殊形式，即在向量空间中选择有限的离散数据作为标签。大多分类算法也都是集中研究二分类算法，多分类可通过多个二分类器组合实现。注意，下面介绍的应用中，ℓs\ell_s的只需要满足前面提到的二次可微即可。

# 回归

在回归任务中，目标函数的ℓs\ell_s通常选择为平方损失函数，这在贝叶斯估计中也可解释去除高斯噪声的残差项，因此回归也可视为一种去噪或恢复的过程。

min⁡D∈D,W∈WEy,x[12∥y−Wα⋆(x,D)∥22]+ν2∥W∥F2\min_{\mathbf D \in \mathcal D, \mathbf W \in \mathcal W} \mathbb E_{\mathbf y,\mathbf x} \Big[\frac{1}{2}\|\mathbf y-\mathbf W \boldsymbol\alpha^\star (\mathbf x,\mathbf D)\|_2^2\Big]+\frac{\nu}{2}\|\mathbf W\|_F^2

当然，ℓs\ell_s也可使用其他的二次可微损失函数来衡量y\mathbf y与Wα⋆(x,D)\mathbf W \boldsymbol\alpha^\star (\mathbf x,\mathbf D)的差异性。

# 二分类

设置标签集为Y={−1;+1}\mathcal Y=\{-1; +1\}，ℓs\ell_s使用logistic回归损失函数来表示标签yy与特征α⋆(x,D)\boldsymbol\alpha^\star(\mathbf x,\mathbf D)之间的关系。对应的线性模型如下：

min⁡w∈Rp,D∈DEy,x[log⁡(1+e−yw⊤α⋆(x,D))]+ν2∥w∥22\min_{\mathbf w \in \mathbb R^p,\mathbf D \in \mathcal D} \mathbb E_{y,\mathbf x} \Big[\log\big(1+e^{-y \mathbf w^\top \boldsymbol\alpha^\star(\mathbf x,\mathbf D)}\big)\Big]+\frac{\nu}{2}\|\mathbf w\|_2^2

求解得到最优解(w,D)(\mathbf w,\mathbf D)后，对新的样本x\mathbf x，计算sgn(w⊤α⋆(x,D))\text{sgn}(\mathbf w^\top \boldsymbol\alpha^\star(\mathbf x,\mathbf D))作为预测的类别。此外还有一种双线性的矩阵变体模型，利用x⊤Wα⋆(x,D)\mathbf x^\top \mathbf W \boldsymbol\alpha^\star(\mathbf x,\mathbf D)来判断类别标签。

min⁡w∈Rm×p,D∈DEy,x[log⁡(1+e−yx⊤Wα⋆(x,D))]+ν2∥W∥F2\min_{\mathbf w \in \mathbb R^{m \times p},\mathbf D \in \mathcal D} \mathbb E_{y,\mathbf x}\Big[\log\big(1+e^{-y \mathbf x^\top \mathbf W \boldsymbol\alpha^\star(\mathbf x,\mathbf D)}\big)\Big] + \frac{\nu}{2}\|\mathbf W\|_F^2

线性模型(向量形式)需要学习pp个参数，而双线性模型(矩阵形式)需要学习pmpm个参数，因此双线性模型能学习到的特征比线性更丰富，但也可能出现过拟合的问题。

# 优化

与非监督字典学习方式一样，总的优化问题对所有变量而言非凸，但对每个变量是凸的，因此优化算法一般采用交替迭代方式。这便需要将原问题划分为多个可解的子问题，然后计算各自的梯度即可。

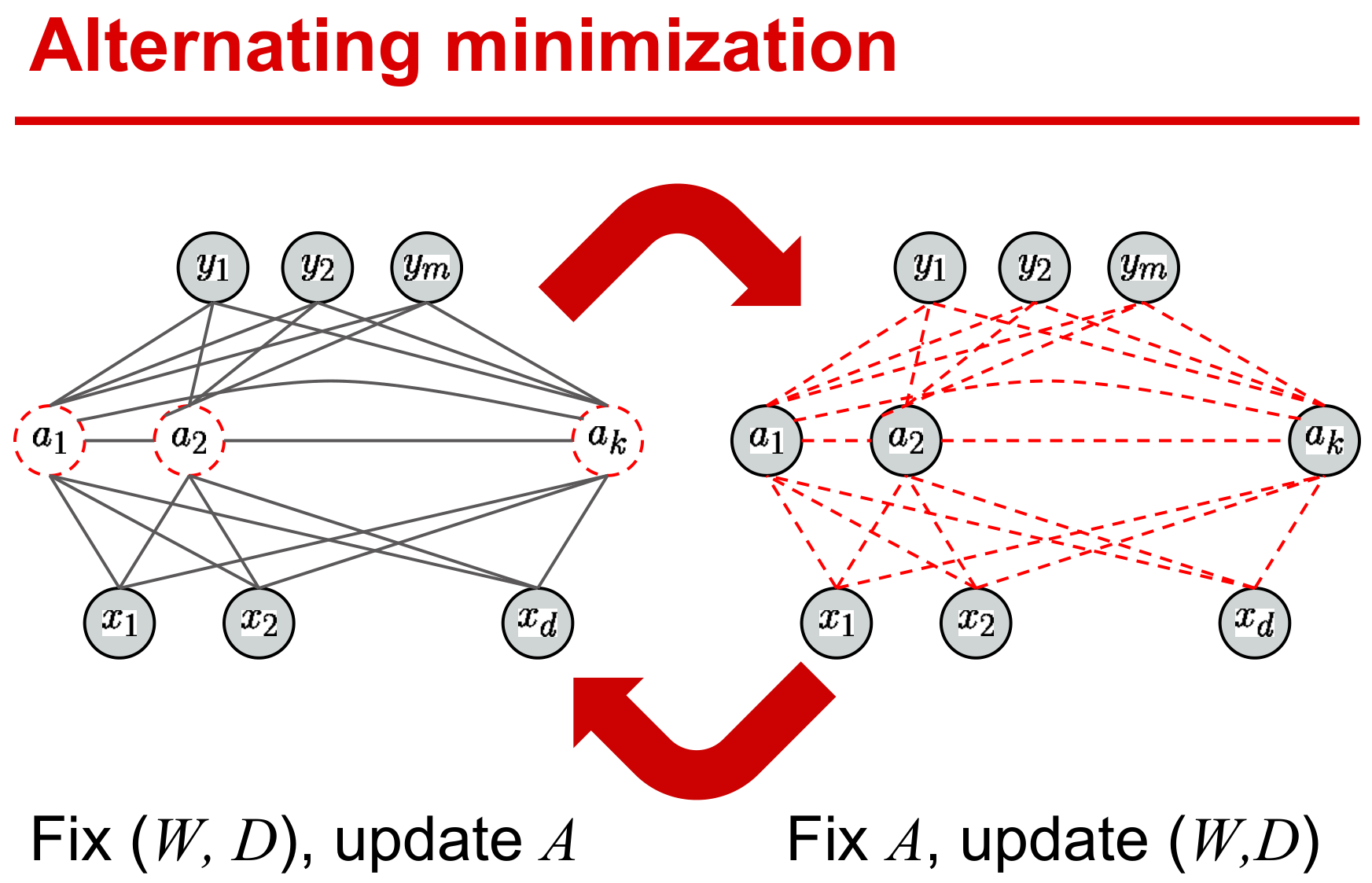
# 函数求导

满足三个基本假设下，函数f(D,W)≜Ey,x[ℓs(y,W,α⋆(x,D))]f(\mathbf D,\mathbf W) \triangleq \mathbb E_{\mathbf y,\mathbf x}[\ell_s (\mathbf y,\mathbf W,\boldsymbol\alpha^\star(\mathbf x,\mathbf D))]是可微的，其导数为

{∇Wf(D,W)=Ey,x[∇Wℓs(y,W,α⋆)],∇Df(D,W)=Ey,x[−Dβ⋆α⋆⊤+(x−Dα⋆)β⋆⊤],\left\{ \begin{aligned} \nabla_\mathbf W f(\mathbf D,\mathbf W) & = \mathbb E_{\mathbf y,\mathbf x}[\nabla_\mathbf W \ell_s(\mathbf y,\mathbf W,\boldsymbol\alpha^\star)], \\ \nabla_\mathbf D f(\mathbf D,\mathbf W) & = \mathbb E_{\mathbf y,\mathbf x}[-\mathbf D\boldsymbol\beta^\star\boldsymbol\alpha^{\star\top} + (\mathbf x-\mathbf D\boldsymbol\alpha^\star) \boldsymbol\beta^{\star\top}], \\ \end{aligned} \right.

记Λ\Lambda为稀疏编码α⋆(x,D)\boldsymbol\alpha^\star(\mathbf x,\mathbf D)的非零系数指标集，上式中向量β⋆\boldsymbol\beta^{\star}的最优条件为

{βΛC⋆=0βΛ⋆=(DΛ⊤DΛ+λ2I)−1∇αΛℓs(y,W,α⋆)\left \{\begin{aligned} &\boldsymbol\beta^\star_{\Lambda^C} = 0 \\ &\boldsymbol\beta^\star_{\Lambda} = (\mathbf D_\Lambda^\top \mathbf D_\Lambda+\lambda_2 \mathbf I)^{-1} \nabla_{\boldsymbol\alpha_\Lambda} \ell_s(\mathbf y,\mathbf W,\boldsymbol\alpha^\star)\\ \end{aligned} \right.

满足三个基本假设下，函数f(D,W,Z)≜Ey,x[ℓs(y,W,α⋆(Zx,D))]f(\mathbf D,\mathbf W,\mathbf Z) \triangleq \mathbb E_{\mathbf y,\mathbf x}[\ell_s (\mathbf y,\mathbf W,\boldsymbol\alpha^\star(\mathbf Z\mathbf x,\mathbf D))]是可微的，其导数为

{∇Wf(D,W)=Ey,x[∇Wℓs(y,W,α⋆)],∇Df(D,W)=Ey,x[−Dβ⋆α⋆⊤+(Zx−Dα⋆)β⋆⊤],∇Zf(D,W)=Ey,x[Dβ⋆x⊤],\left\{ \begin{aligned} \nabla_\mathbf W f(\mathbf D,\mathbf W) & = \mathbb E_{\mathbf y,\mathbf x}[\nabla_\mathbf W \ell_s(\mathbf y,\mathbf W,\boldsymbol\alpha^\star)], \\ \nabla_\mathbf D f(\mathbf D,\mathbf W) & = \mathbb E_{\mathbf y,\mathbf x}[-\mathbf D\boldsymbol\beta^\star\boldsymbol\alpha^{\star\top} + (\mathbf Z\mathbf x-\mathbf D\boldsymbol\alpha^\star) \boldsymbol\beta^{\star\top}], \\ \nabla_\mathbf Z f(\mathbf D,\mathbf W) & = \mathbb E_{\mathbf y,\mathbf x}[\mathbf D\boldsymbol\beta^\star\mathbf x^\top], \\ \end{aligned} \right.

# 算法

随机梯度下降算法是一类典型应对含有期望项的目标函数。下面给一个投影一阶随机梯度下降算法流程。

说明：

  • step 3中采用一种典型的同伦法LARS算法来解决elastic-net稀疏优化问题

  • 矩阵(DΛ⊤DΛ+λ2I)−1(\mathbf D_\Lambda^\top \mathbf D_\Lambda+\lambda_2\mathbf I)^{-1}具有Cholesky分解形式，可快速计算β⋆\boldsymbol\beta^\star

  • 学习率ρt\rho_t采用启发式方式选择：min⁡(ρ,ρt0/t)\min(\rho,\rho t_0/t)

    • 当t<t0t < t_0，使用常数学习率ρ\rho
    • 当t>t0t > t_0，学习率每次递减1/t1/t

  • 采用小批量策略(η>1\eta > 1)提高算法的收敛速度

  • 字典的初值可选用无监督学习获得，可使用SPAMS工具箱。

# 两个推广模型的修改

前面有输入数据的线性变换和半监督学习的两个改进版本，算法部分只需要修改其中对应步骤。

  • 输入数据的线性变换关于Z\mathbf Z的梯度

Z←ΠZ[Z−ρt(Dβ⋆x⊤+ν2Z)],\mathbf Z \leftarrow \Pi_{\mathcal Z}\Big[\mathbf Z - \rho_t (\mathbf D\boldsymbol\beta^\star\mathbf x^{\top}+\nu_2\mathbf Z)\Big],

  • 半监督学习关于D\mathbf D的梯度

D←ΠD[D−ρt((1−μ)(−Dβ⋆α⋆⊤+(xt−Dα⋆)β⋆⊤)+μ(−(xt′−Dα⋆′)α⋆′⊤))]\begin{aligned} \mathbf D \leftarrow \Pi_{\mathcal D}\Big[\mathbf D - \rho_t \Big( &(1-\mu) \big(-\mathbf D \boldsymbol\beta^\star \boldsymbol\alpha^{\star\top} + (\mathbf x_t-\mathbf D \boldsymbol\alpha^\star)\boldsymbol\beta^{\star\top}\big) \\ &+ \mu\big(-(\mathbf x^\prime_t-\mathbf D \boldsymbol\alpha^{\star\prime})\boldsymbol\alpha^{\star\prime\top}\big) \Big) \Big] \end{aligned}

# 小结

本文给出一个任务驱动字典学习的框架，给出一个通用的求解算法，并从理论上给出优化最优性条件（见附录）。文章虽然是12年的文章，但是目前在其他邻域没有见到类似的任务驱动学习范式，另外最近张量表示比较火，可是做下张量形式的任务驱动字典学习。

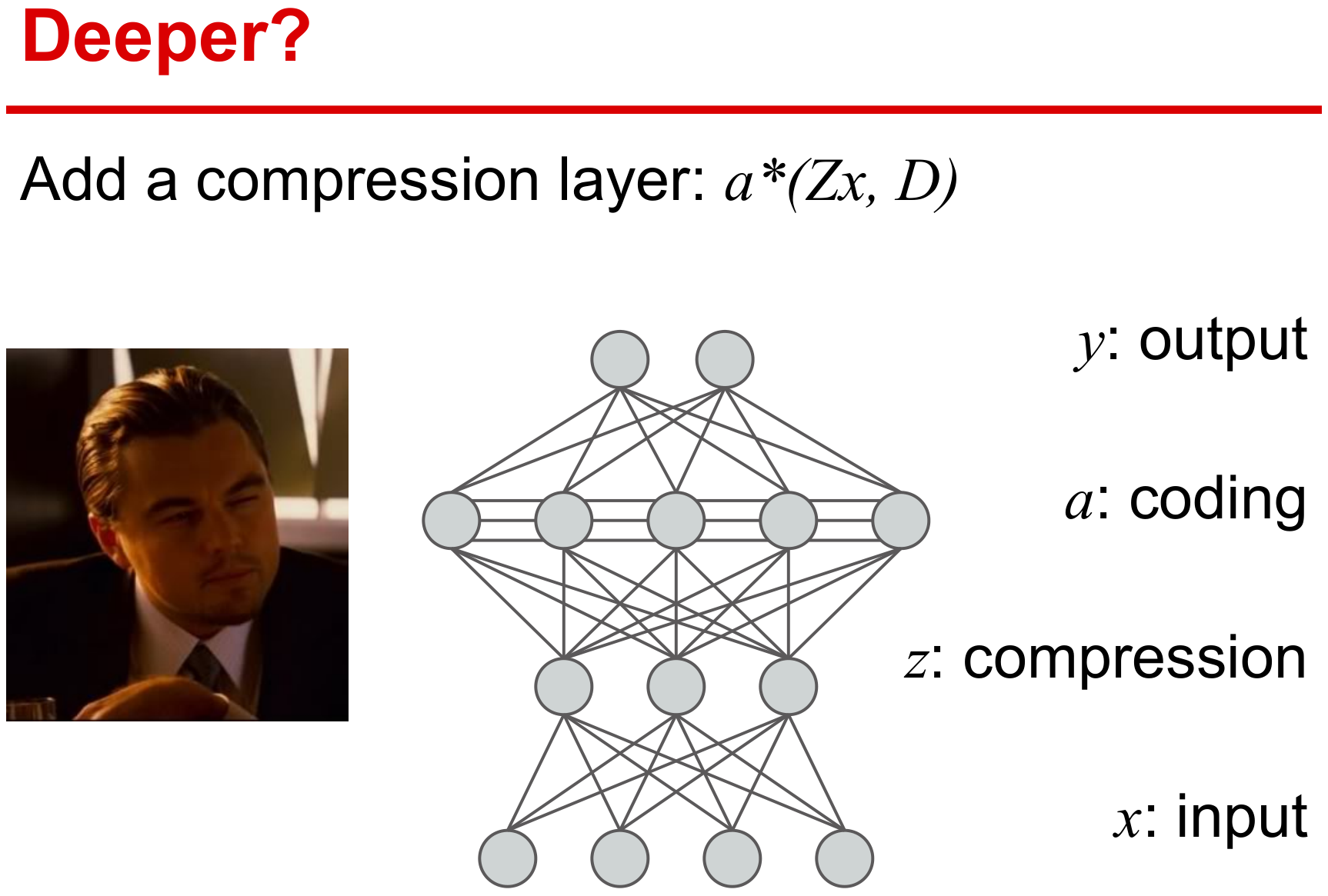
另外slide[2:1]里给了一个深度的展望，这个目前有一些卷积稀疏编码网络的工作（见Elad组[3]），后面如果有精力可以再写写这些方面的文章。

# References

  1. J. Mairal, F. Bach and J. Ponce.Task-Driven Dictionary Learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 34, no. 4, pp. 791-804, 2012, doi: 10.1109/TPAMI.2011.156. ↩︎

  2. Slide: http://cseweb.ucsd.edu/~dasgupta/254-deep/brian.pdf (opens new window) ↩︎ ↩︎

  3. Michael Elad Homepage: https://elad.cs.technion.ac.il (opens new window) ↩︎

联合降维和字典学习