# 写在前面

介绍稀疏主成分分析算法(Sparse Principal Component Analysis)[1]

# 线性回归模型

# PCA

The Elements of Statistical Learning 14.5里通过线性拟合的角度阐述了主成分的概念，这在SPCA里起到一个辅助理解的作用，在此进行补充。

Rp\mathbb R^p空间中数据基x1,x2,…,xN{x_1,x_2,\ldots,x_N}的主成分是秩为k(<p)k(<p)的最佳线性近似序列（正交投影得到线性子空间）

f(λ)=μ+Vkλf(\lambda)= \mu + V_k \lambda

通过重构误差最小二乘对原始数据进行拟合操作

min⁡μ,λi,Vk∑i=1N∥xi−μ−Vkλi∥2\min_{\mu,\lambda_i,V_k} \sum_{i=1}^N \|x_i - \mu- V_k \lambda_i\|^2

令目标函数对μ\mu和λi\lambda_i的偏导为00可得

μ^=xˉ,λ^=VkT(xi−xˉ)\hat\mu = \bar x, \quad\hat\lambda = V_k^T(x_i-\bar x)

同时实现会对数据进行去均值化处理，即xˉ=0\bar x = 0，因此问题转化为对正交矩阵VqV_q优化

min⁡Vk∑i=1N∥xi−VkVkTxi∥2\min_{V_k} \sum_{i=1}^N \|x_i - V_k V_k^Tx_i\|^2

其中Hk×k=VkVkTH_{k\times k} = V_k V_k^T为投影矩阵，并将点xix_i映射至秩为kk的重构点Hk×kxiH_{k\times k} x_i，正交投影后的空间是由矩阵VkV_k的列所张成的子空间。

# Lasso

在最小二乘的惩罚下添加对回归系数的ℓ1\ell_1范数的约束

β^lasso=arg⁡min⁡β∥Y−∑j=1pXjβj∥2+λ∑j=1p∣βj∣\hat\beta_{\text{lasso}} = \arg\min_\beta \|Y - \sum_{j=1}^p X_j \beta_j\|^2 + \lambda \sum_{j=1}^p |\beta_j|

  • 可通过最小角度回归LARS算法高效求解。

  • 不适于样本少而维数高的变量选择，回归系数至多有nn个非零项，这是因为凸优化问题的性质。

  • 除非系数的ℓ1\ell_1范数的边界小于某个值(由权衡参数λ\lambda确定)，否则Lasso不是良定义的(well-defined)。

  • Lasso无法进行分组变量(grouped variables)选择，它倾向于从组中选择一个变量，而忽略其他变量。

# Elastic Net

为了利用所有变量的信息，对岭回归和lasso进行凸组合

β^en=(1+λ2)arg⁡min⁡β∥Y−∑j=1pXjβj∥2+λ2∑j=1p∣βj∣2+λ1∑j=1p∣βj∣\begin{aligned} \hat\beta_{\text{en}} = (1+\lambda_2)&\arg\min_\beta \|Y - \sum_{j=1}^p X_j \beta_j\|^2 \\ &+ \lambda_2 \sum_{j=1}^p |\beta_j|^2 + \lambda_1 \sum_{j=1}^p |\beta_j| \end{aligned}

  • LARS-EN算法高效求解。
  • 当λ2=0\lambda_2 = 0时，Elastic Net退化为Lasso。
  • 引入的二次项
    • 去除变量选择个数的限制，即适合样本少而维数高的情况
    • 有利于分组变量选择(grouping effect)
    • 稳定了ℓ1\ell_1正则化的路径

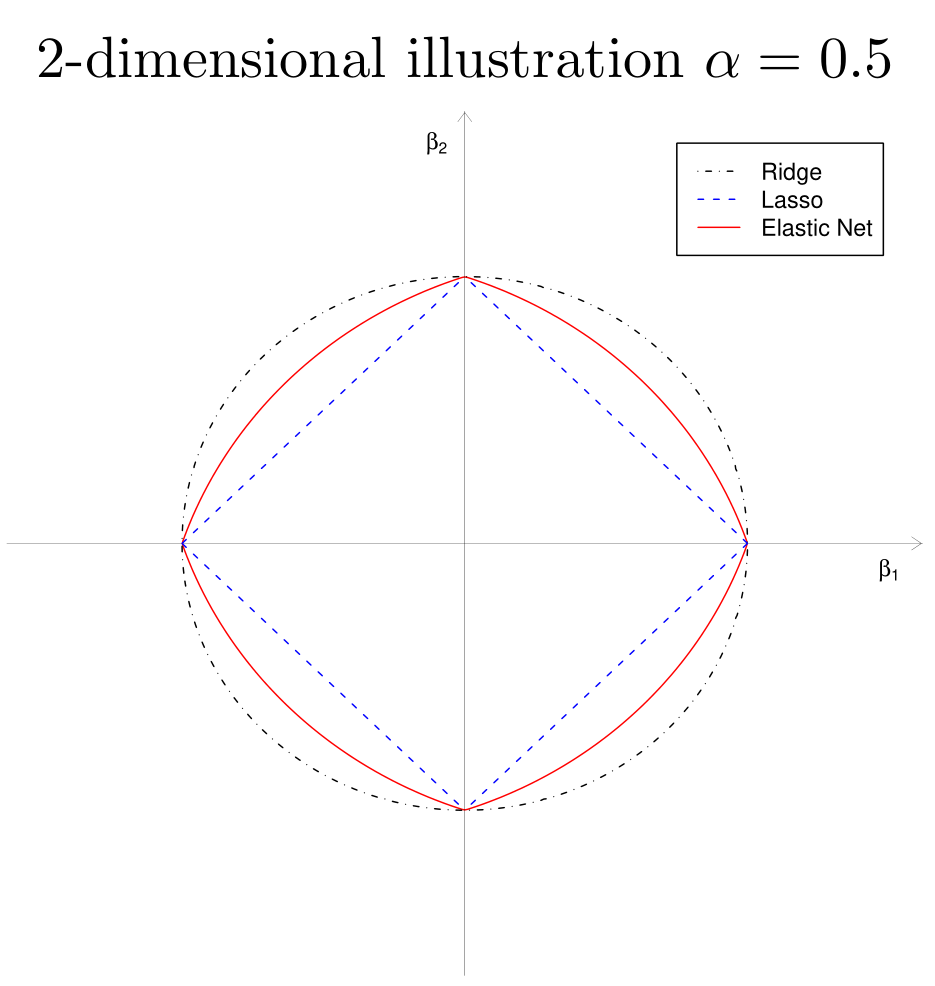
# Elastic Net 正则化的几何性质

J(β)=α∥β∥2+(1−α)∥β∥1≤tJ(\beta) = \alpha \|\beta\|^2 + (1 - \alpha)\|\beta\|_1 \leq t

  • 顶点的奇异性（sparsity）
  • 严格凸的边，凸度的强度随α\alpha而变化（grouping）

# 稀疏主成分分析(SPCA)

# 主成分的岭回归

从PCA出发X=UDVT\mathrm X = \mathrm U \mathrm D \mathrm V^T，对主成分Zi=UiDiiZ_i = U_i D_{ii}进行简单的岭回归

β^ridge=arg⁡min⁡β∥Zi−Xβ∥2+λ∥β∥2\hat\beta_{\text{ridge}} = \arg\min_\beta \|Z_i -\mathrm X\beta\|^2 + \lambda \|\beta\|^2

则归一化的系数v^=β^ridge∥β^ridge∥\hat v = \frac{\hat\beta_{\text{ridge}}}{\|\hat\beta_{\text{ridge}}\|}与因子载荷相等，即v^=Vi\hat v = V_i。这表明奇异值分解得到右奇异向量与主成分的岭回归有潜在的关系，这一结论也不难证明。

由XTX=VD2VT\mathrm X^T \mathrm X = \mathrm V \mathrm D^2 \mathrm V^T和岭回归的显示表达式

β^ridge=(XTX+λI)−1XT(XVi)=Dii2Dii2+λVi\begin{aligned} \hat\beta_{\text{ridge}} &= (\mathrm X^T \mathrm X + \lambda \mathrm I)^{-1} \mathrm X^T (\mathrm X \mathrm V_i)\\ &= \frac{D_{ii}^2}{D_{ii}^2 + \lambda}\mathrm V_i \end{aligned}

# 稀疏近似

下面在岭回归的基础上加上ℓ1\ell_1正则化得到去除倍数的Elastic Net

arg⁡min⁡β∥Zi−Xβ∥2+λ∥β∥2+λ1∥β∥1\arg\min_\beta \|Z_i -\mathrm X\beta\|^2 + \lambda \|\beta\|^2 + \lambda_1 \|\beta\|_1

对得到的结果单位化V^1=β^∥β^∥\hat V_1 = \frac{\hat\beta}{\|\hat\beta\|}并称为右奇异向量ViV_i的近似，称XV^1\mathrm X \hat V_1为第ii个主成分的近似。显然，λ1\lambda_1越大，得到的β^\hat\beta越稀疏，因此V^1\hat V_1越稀疏。

# 岭回归

考虑一个岭回归问题

β^=arg⁡min⁡β∥y−Xβ∥2+λ∥β∥2\hat \beta = \arg\min_\beta \|\mathrm y-\mathrm X\beta\|^2 + \lambda \|\beta\|^2

设目标函数的导数为00可得最优解的必要条件

−XT(y−Xβ^)+λβ^=0⇒β^=(XTX+λI)−1XTy\begin{aligned} &-\mathrm X^T (\mathrm y-\mathrm X\hat\beta) + \lambda \hat\beta = 0 \\ \Rightarrow\quad &\hat\beta = (\mathrm X^T\mathrm X + \lambda \mathrm I)^{-1}\mathrm X^Ty \end{aligned}

因此目标函数

∥y−Xβ^∥2+λ∥β^∥2=(y−Xβ^)T(y−Xβ^)+λβ^Tβ^=(y−Xβ^)Ty−(y−Xβ^)TXβ^+Xβ^)TXβ^=yT(I−X(XT+λI)−1XT)y\begin{aligned} & \|\mathrm y-\mathrm X\hat\beta\|^2 + \lambda \|\hat\beta\|^2\\ & = (\mathrm y-\mathrm X\hat\beta)^T(\mathrm y-\mathrm X\hat\beta) + \lambda \hat\beta^T\hat\beta\\ & = (\mathrm y-\mathrm X\hat\beta)^T\mathrm y -(\mathrm y-\mathrm X\hat\beta)^T\mathrm X\hat\beta + \mathrm X\hat\beta)^T\mathrm X\hat\beta \\ & = \mathrm y^T(\mathrm I - \mathrm X(\mathrm X^T +\lambda \mathrm I)^{-1}\mathrm X^T)\mathrm y \end{aligned}

记岭回归算子Sλ=X(XT+λI)−1XT\mathrm S_\lambda = \mathrm X(\mathrm X^T +\lambda \mathrm I)^{-1}\mathrm X^T，则满足Xβ^=Sλy\mathrm X\hat\beta = \mathrm S_\lambda \mathrm y 。

# PCA重铸为回归模型

上面的优化问题都依赖PCA的结果，下面提出独立于SVD分解主成分的优化问题，建立PCA模型与回归型问题的联系。

首先考虑单个主成分。以第一个主成分为例，对任意λ>0\lambda > 0

(α^,β^)=arg⁡min⁡α,β∑i=1n∥xi−αβTxi∥2+λ∥β∥2s.t.∥α∥2=1\begin{aligned} (\hat \alpha, \hat \beta) = &\arg\min_{\alpha,\beta} \sum_{i=1}^n \|\mathrm x_i - \alpha\beta^T \mathrm x_i \|^2 + \lambda \|\beta\|^2 \\ &\text{s.t.} \|\alpha\|^2 = 1 \end{aligned}

则β^∝V1\hat\beta \propto V_1。这一结论的矩阵版本可以同时获得所有的主成分。记

Ap×k=[α1,…,αk],Bp×k=[β1,…,βk]\mathrm A _{p \times k} = [\alpha_1, \ldots, \alpha_k], \mathrm B_{p \times k} = [\beta_1, \ldots, \beta_k]

对任意λ>0\lambda > 0

(A^,B^)=arg⁡min⁡A,B∑i=1n∥xi−ABTxi∥2+λ∑j=1k∥βj∥2s.t.ATA=Ik×k\begin{aligned} (\mathrm{\hat A}, \mathrm{\hat B}) =& \arg\min_{\mathrm A,\mathrm B} \sum_{i=1}^n \|\mathrm x_i - \mathrm A\mathrm B^T \mathrm x_i \|^2 \\ &+ \lambda \sum_{j=1}^k\|\beta_j\|^2 \quad \text{s.t.} \mathrm A^T \mathrm A = \mathrm I_{k \times k} \end{aligned}

则β^j∝Vj\hat\beta_j \propto V_j。

显然，令B=A\mathrm B = \mathrm A，则∑i=1n∥xi−ABTxi∥2=∑i=1n∥xi−AATxi∥2\sum_{i=1}^n \|\mathrm x_i - \mathrm A\mathrm B^T \mathrm x_i \|^2 = \sum_{i=1}^n \|\mathrm x_i - \mathrm A\mathrm A^T \mathrm x_i \|^2，这是一个典型的基于重构误差的PCA模型。由于酉阵不改变矩阵的ℓ2\ell_2范数，但半酉阵不具备这一性质，因此需要对A\mathrm A补全为[A;A⊥][\mathrm A; \mathrm A_\bot]，其中A⊥\mathrm A_\bot是与A\mathrm A正交的半酉阵。

∑i=1n∥xi−ABTxi∥2=∥X−XBAT∥2=∥(X−XBAT)[A;A⊥]∥2=∥(X−XBAT)A⊥∥2+∥(X−XBAT)A∥2=∥XA⊥∥2+∥XA−XB∥2=∥XA⊥∥2+∑j=1k∥Xαj−Xβj∥2\begin{aligned} &\sum_{i=1}^n \|\mathrm x_i - \mathrm A\mathrm B^T \mathrm x_i \|^2 \\ =& \|\mathrm X - \mathrm X \mathrm B \mathrm A^T\|^2\\ =& \|(\mathrm X - \mathrm X \mathrm B \mathrm A^T)[\mathrm A; \mathrm A_\bot]\|^2\\ =& \|(\mathrm X - \mathrm X \mathrm B \mathrm A^T)\mathrm A_\bot\|^2 + \|(\mathrm X - \mathrm X \mathrm B \mathrm A^T)\mathrm A\|^2\\ =& \|\mathrm X \mathrm A_\bot\|^2 + \|\mathrm X \mathrm A- \mathrm X \mathrm B \|^2\\ =& \|\mathrm X \mathrm A_\bot\|^2 + \sum_{j=1}^k\|\mathrm X \alpha_j- \mathrm X \beta_j \|^2\\ \end{aligned}

  • 若矩阵A\mathrm A固定，上述优化问题转化为kk个岭回归问题

arg⁡min⁡B∑j=1k∥Xαj−Xβj∥2+λ∥βj∥2\arg\min_{\mathrm B} \sum_{j=1}^k\|\mathrm X \alpha_j- \mathrm X \beta_j \|^2 + \lambda \|\beta_j\|^2

由岭回归的显示解可得

B^=(XTX+λI)−1XTXA\mathrm {\hat B} = (\mathrm X^T\mathrm X + \lambda \mathrm I)^{-1}\mathrm X^T \mathrm X \mathrm A

  • 固定矩阵B^\mathrm {\hat B}，目标函数关于变量A\mathrm A的优化问题为

arg⁡min⁡A∥X−XB^AT∥2+λ∑j=1k∥βj∥2=arg⁡min⁡Atr(XTX)−tr(ATXTSλXA)=arg⁡max⁡Atr(ATXTSλXA)s.t.ATA=Ik×k\begin{aligned} &\arg\min_{\mathrm A}\|\mathrm X - \mathrm X \mathrm {\hat B} \mathrm A^T\|^2 + \lambda \sum_{j=1}^k\|\beta_j\|^2 \\ =& \arg\min_{\mathrm A}\text{tr}(\mathrm X^T \mathrm X) - \text{tr}(\mathrm A^T\mathrm X^T \mathrm S_\lambda \mathrm X\mathrm A)\\ =& \arg\max_{\mathrm A} \text{tr}(\mathrm A^T\mathrm X^T \mathrm S_\lambda \mathrm X\mathrm A) \quad \text{s.t.} \mathrm A^T \mathrm A = \mathrm I_{k \times k} \end{aligned}

因此A\mathrm A为矩阵XTSλX\mathrm X^T \mathrm S_\lambda \mathrm X的最大的kk个特征值对应的特征向量。设X=UDVT\mathrm X = \mathrm U \mathrm D \mathrm V^T，则

XTSλX=VD2(D2+λI)−1D2VT\mathrm X^T \mathrm S_\lambda \mathrm X = \mathrm V\mathrm D^2(\mathrm D^2+\lambda \mathrm I)^{-1}\mathrm D^2 \mathrm V^T

故A^=V[,1:k]\mathrm {\hat A} = \mathrm V[, 1:k]，这也将岭回归与PCA建立联系，而[A;A⊥]=V[\mathrm A; \mathrm A_\bot] = \mathrm V。

  • 返回去再看B^\mathrm {\hat B}与V\mathrm V成比例关系。

β^j=(XTX+λI)−1XTXVj∝Vj\hat \beta_j = (\mathrm X^T\mathrm X + \lambda \mathrm I)^{-1}\mathrm X^T \mathrm X V_j \propto V_j

# 岭回归与Lasso的组合:SPCA

(A^,B^)=arg⁡min⁡A,B∑i=1n∥xi−ABTxi∥2+λ∑j=1k∥βj∥2+∑j=1kλ1,j∥βj∥1s.t.ATA=Ik×k\begin{aligned} (\mathrm{\hat A}, \mathrm{\hat B}) = &\arg\min_{\mathrm A,\mathrm B} \sum_{i=1}^n \|\mathrm x_i - \mathrm A\mathrm B^T \mathrm x_i \|^2 + \lambda \sum_{j=1}^k\|\beta_j\|^2\\ & + \sum_{j=1}^k\lambda_{1,j}\|\beta_j\|_1 \quad \text{s.t.} \mathrm A^T \mathrm A = \mathrm I_{k \times k} \end{aligned}

该问题对两个变量不是凸的，但对单个变量而固定另一个变量时是凸的，因此采用交替方式迭代。

  • 给定A\mathrm A更新B\mathrm B

arg⁡min⁡B∑i=1n∥xi−ABTxi∥2⟺arg⁡min⁡B∑j=1k∥Xαj−Xβj∥2\begin{aligned} &\arg\min_{\mathrm B} \sum_{i=1}^n \|\mathrm x_i - \mathrm A\mathrm B^T \mathrm x_i \|^2 \\ \iff &\arg\min_{\mathrm B} \sum_{j=1}^k \|\mathrm X \alpha_j - \mathrm X\beta_j\|^2 \end{aligned}

令Yj∗=XαjY_j^* = \mathrm X \alpha_j，优化问题可转化为kk个Elastic net 子问题

β^j=arg⁡min⁡β∥Yj∗−Xβ∥2+λ∥β∥2+λ1,j∥β∥1=arg⁡min⁡β(αj−β)TXTX(αj−β)+λ∥β∥2+λ1,j∥β∥1\begin{aligned} \hat \beta_j =& \arg\min_\beta \|Y_j^* - \mathrm X\beta\|^2 + \lambda \|\beta\|^2 + \lambda_{1,j}\|\beta\|_1\\ =& \arg\min_\beta (\alpha_j - \beta)^T \mathrm X^T\mathrm X(\alpha_j - \beta) + \lambda \|\beta\|^2 + \lambda_{1,j}\|\beta\|_1 \end{aligned}

  • 给定B\mathrm B更新A\mathrm A

子优化问题为

arg⁡min⁡A∥X−XBTA∥2s.t.ATA=Ik×k\arg\min_{\mathrm A} \|\mathrm X - \mathrm X \mathrm B^T \mathrm A \|^2 \quad \text{s.t.} \mathrm A^T \mathrm A = \mathrm I_{k \times k}

利用Procrustes旋转的降秩表示结论，记SVD:(XTX)B=UDVT(\mathrm X^T \mathrm X) \mathrm B= \mathrm U\mathrm D \mathrm V^T，则解为

A^=UVT\mathrm{\hat A} = \mathrm U \mathrm V^T

note: 上面岭回归中∥X−XB^AT∥2+λ∑j=1k∥βj∥2\|\mathrm X - \mathrm X \mathrm {\hat B} \mathrm A^T\|^2 + \lambda \sum_{j=1}^k\|\beta_j\|^2化成了特征分解问题tr(ATXTSλXA)\text{tr}(\mathrm A^T\mathrm X^T \mathrm S_\lambda \mathrm X\mathrm A)，这是因为β^j\hat\beta_j与αj\alpha_j有关（岭回归算子），但此处的β^j\hat\beta_j是通过LARS-EN算法求解，与αj\alpha_j无直接关系，因此两个问题本质上有区别。

# 补充：Reduced Rank Procrustes Rotation

设MTNM^T N的SVD:MTN=UDVTM^T N = U D V^T，则对约束优化问题

arg⁡min⁡A∥M−NAT∥2s.t.ATA=Ik×k\arg\min_{ A} \| M - N A^T\|^2 \quad \text{s.t.} A^T A = I_{k \times k}

下面对目标函数的范数展开，并利用正交约束和迹函数的性质可得

∥M−NAT∥2=tr(MTM)−2tr(MTNAT)+tr(ANTNAT)∝−2tr(MTNAT)+tr(NTNATA)∝−2tr(MTNAT)=−2tr(UDVTAT)=−2tr(UDA∗T)=−2tr(A∗TUD)\begin{aligned} &\| M - N A^T\|^2 \\ & = \text{tr}(M^T M) - 2\text{tr}(M^T NA^T) + \text{tr}(AN^TNA^T) \\ &\propto- 2\text{tr}(M^T NA^T) + \text{tr}(N^TNA^TA)\\ &\propto -2\text{tr}(M^T NA^T)\\ &= -2\text{tr}(UDV^TA^T)\\ &= -2\text{tr}(UD{A^*}^T)\\ &= -2\text{tr}({A^*}^T UD)\\ \end{aligned}

其中A∗=AVA^* = AV满足A∗TA∗=I{A^*}^T A^* = I，对角阵DD由奇异值组成，因此优化问题寻找A∗TU{A^*}^T U对角元素为最大正数的条件。利用Cauchy-Schwartz不等式可知，当A∗=UA^* = U时取最优解。因此A^=UVT{\hat A} = U V^T。

# 算法流程

# 方差调整

传统PCA算法得到的主成分是无关的，载荷是相互正交的，但是稀疏化后无关性不在满足，这是因为Z^TZ^\mathrm {\hat Z}^T \mathrm {\hat Z}不是严格的对角矩阵，为此需要对每个主成分做类似Schmidt 正交化，对每个主成分减去前面特征值方向的分量，从而保证正交性

Z^j⋅1,…,j−1=Z^j−H1,…,j−1Z^j\mathrm {\hat Z}_{j\cdot 1,\ldots,j-1} = \mathrm {\hat Z}_{j} - \mathrm H_{1,\ldots,j-1} \mathrm {\hat Z}_{j}

其中H1,…,j−1\mathrm H_{1,\ldots,j-1}是投影矩阵，调整后主成分的方差为∑j=1k∥Z^j⋅1,…,j−1∥2=tr(Z^TZ^)\sum_{j=1}^k \|\mathrm {\hat Z}_{j\cdot 1,\ldots,j-1}\|^2 = \text{tr} (\mathrm {\hat Z}^T \mathrm {\hat Z})（如果无关）。

# 少样本高纬度

上面的SPCA算法对p≫np\gg n是适用的，不过计算量会很大，下面通过一刀切的方式进行简化，即令λ→∞\lambda \to \infty。

令V^j(λ)=β^j∥β^j∥\mathrm {\hat V}_j (\lambda) = \frac{\hat \beta_j}{\|\hat \beta_j\|}，

(A^,B^)=arg⁡min⁡A,B−2tr(ATXTXB)+∑j=1k∥βj∥2+∑j=1kλ1,j∥βj∥1s.t.ATA=Ik×k\begin{aligned} (\mathrm{\hat A}, \mathrm{\hat B}) = &\arg\min_{\mathrm A,\mathrm B} -2\text{tr}(\mathrm A^T \mathrm X^T \mathrm X \mathrm B) + \sum_{j=1}^k\|\beta_j\|^2\\ & + \sum_{j=1}^k\lambda_{1,j}\|\beta_j\|_1 \quad \text{s.t.} \mathrm A^T \mathrm A = \mathrm I_{k \times k} \end{aligned}

当λ→∞\lambda \to \infty有V^j(λ)→β^j∥β^j∥\mathrm {\hat V}_j (\lambda) \to \frac{\hat \beta_j}{\|\hat \beta_j\|}。

与SPCA算法相比，只有B^\mathrm{\hat B}的更新从Elastic Net问题变为如下稀疏优化问题

β^j=arg⁡min⁡β−2αjT(XTX)β+∥β∥2+λ1,j∥β∥1\hat \beta_j = \arg\min_\beta -2\alpha_j^T (\mathrm X^T \mathrm X) \beta+\|\beta\|^2+\lambda_{1,j}\|\beta\|_1

其解可通过软阈值算子(soft-thresholding)显示表达

β^j=(∣αjTXTX∣−λ1,j2)+sign(αjTXTX)\hat \beta_j = (|\alpha_j^T \mathrm X^T \mathrm X|-\frac{\lambda_{1,j}}{2})_+ \text{sign} (\alpha_j^T \mathrm X^T \mathrm X)

# 半正定规划

参考A Mathematical Introduction to Data Science的4.4节

  • 传统PCA可表示为

max⁡xxTΣxs.t.∥x∥2=1\max_x x^T \Sigma x \quad \text{s.t.} \quad \|x\|_2 = 1

由于

xTΣx=tr(Σ(xxT))=tr(ΣX)x^T \Sigma x = \text{tr}(\Sigma (xx^T)) = \text{tr}(\Sigma X)

  • 传统PCA等价表示

max⁡Xtr(ΣX)s.t.tr(X)=1,X⪰0\max_X \text{tr}(\Sigma X) \quad \text{s.t.} \quad \text{tr}( X) = 1, X \succeq 0

该优化问题的最优解是第一个主成分矩阵，其秩为11。因此可以递归地对协方差阵Σk=Σ−∑i<kXi\Sigma_k = \Sigma - \sum_{i<k} X_i使用该程序可得到前kk个主成分。

  • 稀疏PCA的半正定规划形式

max⁡Xtr(ΣX)−λ∥X∥1s.t.tr(X)=1,X⪰0\max_X \text{tr}(\Sigma X) - \lambda \|X\|_1 \quad \text{s.t.} \quad \text{tr}( X) = 1, X \succeq 0

其中ℓ1\ell_1范数的凸化(convexification)可以保证主成分的稀疏性，即#Xij≠0\#{X_{ij} \neq 0}非常小。

# 参考文献

  1. Zou H, Hastie T, Tibshirani R, et al. Sparse Principal Component Analysis[J]. Journal of Computational and Graphical Statistics, 2006, 15(2): 265-286. ↩︎

共空间模式