写在前面

介绍核主成分分析算法(Kernel Principal Component Analysis)^[1]

主成分分析

给定$N$个样本$x_i \in \mathbb{R}^p$，假设$\sum_i x_i =0$，样本的协方差矩阵为$\Sigma=\frac{1}{N}\sum_i x_i x_i^T \in \mathbb{R}^{p \times p}$，对其作特征值分解：

$$\Sigma = U \Lambda U^T = \sum_k \lambda_k u_k u_k^T, UU^T = I_p$$

得到降维投影映射$y_i = U_k^T x_i$，其中$U_k\in \mathbb{R}^{p\times k}$为前$k$个特征列向量构成的子矩阵，显然

$$\frac{1}{N}\sum_i y_i y_i^T = \frac{1}{N} \sum_i U_k^T x_i x_i^T U_k = U_k^T \Sigma U_k = U_k^T U \Lambda U^T U_k^T =\Lambda_k$$

其中$\Lambda_k \in \mathbb{R}^{k \times k}$为前$k$个最大的特征值构成的对角矩阵。记样本矩阵$X=[x_1,x_2,\dots,x_N]\in \mathbb{R}^{p \times N}$，以上问题可以用如下优化问题来概述

$$\begin{aligned} &\min\limits_{U_k U_k^T = I_k} \sum_i \|x_i-{\mathcal{P}}_k(x_i)\|^2 \\ & = \min tr(X-{\mathcal{P}}_k(X))^T(X-{\mathcal{P}}_k(X))\\ & = \min tr(X^T(I-{\mathcal{P}}_k)^T(I-{\mathcal{P}}_k)Y)\\ & = \min tr(XX^T(I-{\mathcal{P}}_k)^2)\\ & = \min tr(XX^T(I-{\mathcal{P}}_k))\\ & = \min tr(XX^T) - tr(XX^T U_k U_k^T)\\ & = \max tr(U_k^T XX^T U_k)\\ & = \max tr(U_k^T \Sigma U_k) \\ & =\max tr(\Sigma_k)= \sum_{i=1}^k \lambda_k \end{aligned}$$

其中${\mathcal{P}}_k = U_k U_k^T$是到子空间的投影映射。此时$U_k$的最优解为前$k$个特征向量构成的列酉阵。

线性到非线性

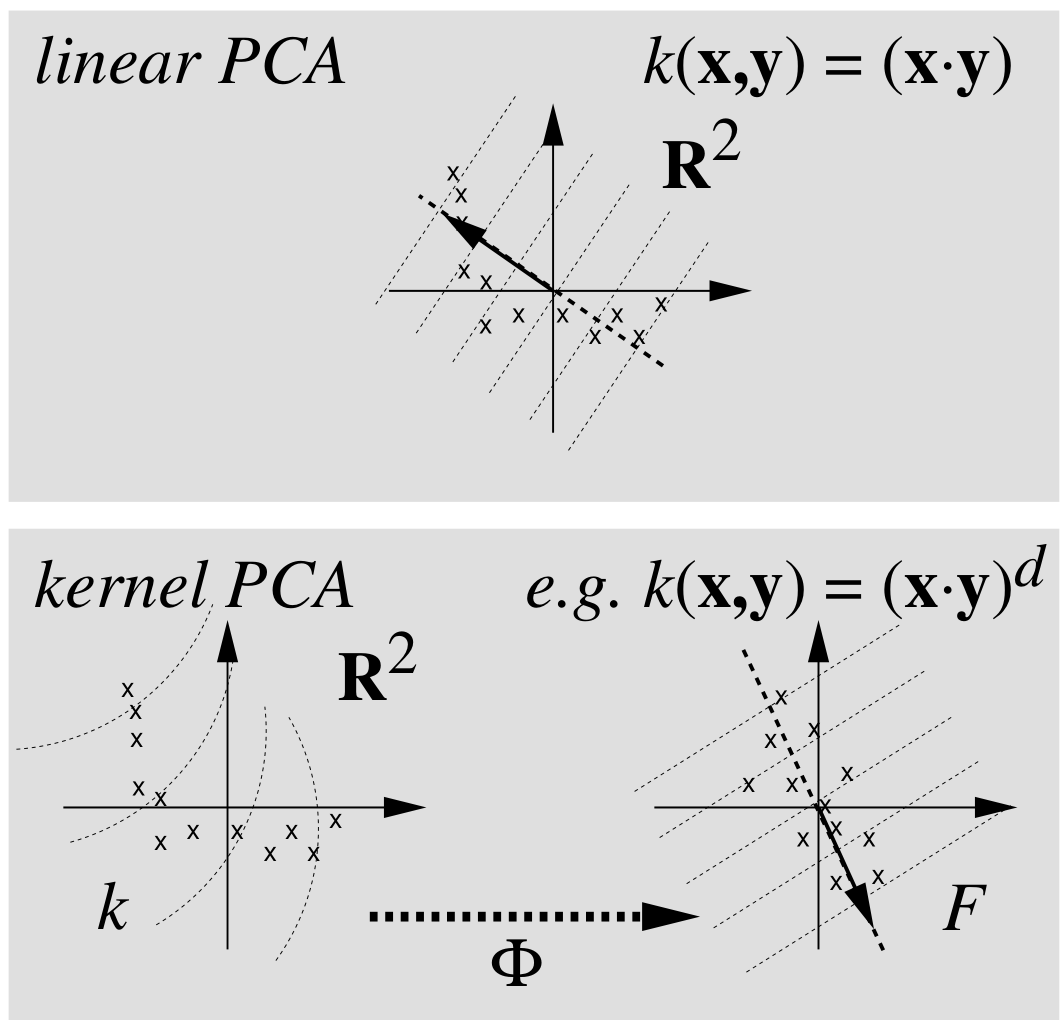
核主成分分析

向量内积$\langle a, b\rangle = a^T b$，求解协方差矩阵的特征方程

$$\lambda u = \Sigma u = (\frac{1}{N}\sum_i x_i x_i^T) u = \frac{1}{N}\sum_i \langle x_i, u \rangle x_i$$

• $$\lambda \langle x_i, u\rangle = \langle x_i, \Sigma u\rangle$$

• $$u = \sum_i \frac{\langle x_i,u \rangle}{\lambda N} x_i = \sum_i \alpha_i x_i$$

引入非线性映射$\Phi :{\mathbb{R}^p \to F, x\mapsto X}$，假设$\sum_i \Phi(x_i)=0$成立，否则可进行中心化处理$\Phi(x_i)=\Phi(x_i)-\frac{1}{N}\sum_j \Phi(x_j)$。对应协方差矩阵为

$$\bar{\Sigma} = \frac{1}{N}\sum_i \Phi(x_i)\Phi(x_i)^T$$

对应特征值方程为$\lambda U = \bar{\Sigma} U$，表明特征向量位于$\Phi(x_1),\cdots,\Phi(x_N)$所张成的空间内，可得以下两个结论：

• $$\lambda \langle \Phi(x_i), U\rangle = \langle\Phi(x_i), \bar{\Sigma} U\rangle$$

• $$U = \sum_j \alpha_j \Phi(x_j)$$

可得

$$\lambda \sum_j \alpha_j \langle \Phi(x_i), \Phi(x_j)\rangle = \frac{1}{N}\sum_{j,k} \alpha_j\langle\Phi(x_i), \Phi(x_k)\rangle \langle\Phi(x_k), \Phi(x_j)\rangle$$

令$K_{ij} = \langle\Phi(x_i), \Phi(x_j)\rangle, \tilde{\lambda} = N \lambda$，

$$K \alpha = \tilde{\lambda}\alpha$$

由于特征向量的单位化，即$U^T U = 1$，可得

$$\sum_{i,j} \alpha_i \alpha_j \langle\Phi(x_i), \Phi(x_j)\rangle = \alpha^T K \alpha = \tilde{\lambda} \alpha^T \alpha =1$$

对于新的样本点$t$，特征空间对应点$\Phi(t)$的投影可表示为

$$\langle U, \Phi(t)\rangle = \sum_j \alpha_j \langle \Phi(x_j), \Phi(t)\rangle = \sum_j \alpha_j K(x_j,t)$$

计算步骤

1. 计算矩阵$K$
2. 计算特征向量并归一化
3. 计算新的样本点对应的特征向量

核函数

不同核函数具有不同的意义，后面会专门写一个核方法、核技巧的总结。

Kernel PCA性质(继承于PCA)

• 前$q$个主成分比其他任意$q$个主成分表示的方差是最大的
• 前$q$个主成分比其他任意$q$个主成分表示的均方误差是最小的
• 主成分具有无关性
• 前$q$个主成分比其他任意$q$个主成分表示的互信息最多

参考文献

---

1. Scholkopf B, Smola A J, Muller K, et al. Nonlinear component analysis as a kernel eigenvalue problem[J]. Neural Computation, 1998, 10(5): 1299-1319. ↩︎