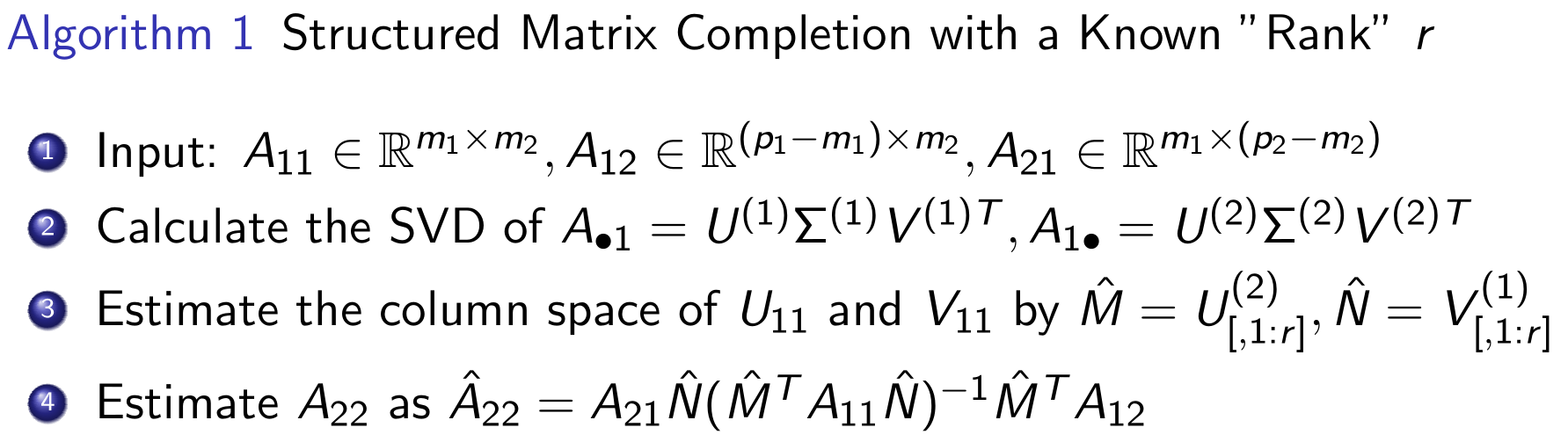写在前面

最近看了些矩阵补全和矩阵结构化的文章，看到张老师主页^[1]上有很多这个方向的成果，下面挑了一个16年的文章^[2]。

Schur 补

给一个分块矩阵

$$\left[\begin{array}{c|c} \mathbf{A}_{11} & \mathbf{A}_{12} \\ \hline \mathbf{A}_{21} & \mathbf{A}_{22} \end{array}\right]$$

• 如果块矩阵$\mathbf{A}_{11}$可逆，则称$\mathbf{A}_{22}-\mathbf{A}_{21}\mathbf{A}_{11}^{-1}\mathbf{A}_{12}$为$\mathbf{A}_{11}$的Schur 补
• 如果块矩阵$\mathbf{A}_{22}$可逆，则称$\mathbf{A}_{11}-\mathbf{A}_{12}\mathbf{A}_{22}^{-1}\mathbf{A}_{21}$为$\mathbf{A}_{22}$的Schur 补

用Schur 补可得到块矩阵的逆

$$\begin{array}{rcl} {\left[\begin{array}{c|c} \mathbf{A}_{11} & \mathbf{A}_{12} \\ \hline \mathbf{A}_{21} & \mathbf{A}_{22} \end{array}\right]^{-1}} =\left[\begin{array}{c|c} \mathbf{I} & \mathbf{0} \\ \hline-\mathbf{A}_{22}^{-1} \mathbf{A}_{21} & \mathbf{I} \end{array}\right]&\times&\\ \left[\begin{array}{c|c} \left(\mathbf{A}_{11}-\mathbf{A}_{12} \mathbf{A}_{22}^{-1} \mathbf{A}_{21}\right)^{-1} & \mathbf{0} \\ \hline \mathbf{0} & \mathbf{A}_{22}^{-1} \end{array}\right]&\times&\left[\begin{array}{c|c} \mathbf{I} & -\mathbf{A}_{12} \mathbf{A}_{22}^{-1} \\ \hline \mathbf{0} & \mathbf{I} \end{array}\right] \end{array}$$

矩阵补全

当观察元素是

• 均匀随机抽样
  • 核范数最小化
• 独立取样但不统一
  • 加权核范数最小化（已知采样分布）
  • 经验加权核范数最小化（未知采样分布）
  • 最大范数最小化（最小二乘）
• 结构化采样？

结构化矩阵补全

目标：给定矩阵的某些行和列来恢复整个矩阵。由于矩阵奇异值关于行、列置换具有不变性，因此可对矩阵$A$进行分块，给定矩阵$A$的部分行$[A_{11}, A_{12}]$和列$[A_{11};A_{21}]$，求解$A_{22}$。

$$A_{p_1\times p_2} = \begin{pmatrix} (A_{11})_{m_2\times m_1} & (A_{12})_{(p_2 - m_2)\times m_1} \\ (A_{21})_{m_2\times {(p_1-m_1)}} & ({\color{red} A_{22}})_{(p_2 - m_2)\times (p_1-m_1)} \end{pmatrix}$$

该补全问题如果不限制矩阵的特征，则存在无穷解。下面考虑近似低秩的先验假设。

精确低秩矩阵恢复

当矩阵$A$的秩为$r$时，记$A_{11}$的奇异值分解为$A_{11} = U\Sigma V^{\intercal}$，如果

$$\text{rank}([A_{11} \; A_{12}] ) = \text{rank}\left(\begin{bmatrix} A_{11}\\ A_{21} \end{bmatrix} \right) = \text{rank}(A) = r$$

则$\text{rank}(A_{11}) = r$，且$A_{22}$可精确求解

$$A_{22} = A_{21}(A_{11})^\dagger A_{12} = A_{21}V(\Sigma)^{-1}U^{\intercal}A_{12}.$$

• 注意在相同条件下，核范数最小化则无法得到$A_{22}$的精确解

$$\hat A_{22} = \arg\min_{B} \left\|\begin{bmatrix} A_{11} & A_{12}\\ A_{21} & B \end{bmatrix}\right\|_\ast$$

• 此外一些其他的变体，例如惩罚的核范数最小化与松弛化的约束核范数最小化对结构化矩阵补全问题求解不稳定。

• 精确的秩先验可以得到显式解，且解的形式简单。

• 对矩阵$A_{11}$产生微小的扰动都会使得$(A_{11})^\dagger$不稳定（非连续性），不适合近似低秩的情形。

近似低秩矩阵恢复

当矩阵$A$的第$r$个奇异值$\sigma_r (A)$与第$r+1$个奇异值$\sigma_{r+1} (A)$存在明显的差异(significant gap)，且拖尾$\left(\sum_{k\geq r+1}\sigma_k^q (A)\right)^{1/q}$特别小，则称矩阵$A$为近似秩$r$。

令分块矩阵$A$的奇异值分解为

$$\begin{aligned} A &= U\Sigma V^{\intercal}\\ &=\begin{pmatrix} U_{11} & U_{12}\\ U_{21} & U_{22}\\ \end{pmatrix} \begin{pmatrix} \Sigma_{1} & 0\\ 0 & \Sigma_{2}\\ \end{pmatrix} \begin{pmatrix} V_{11} & V_{12}\\ V_{21} & V_{22}\\ \end{pmatrix}^{\intercal}\\ &=\begin{pmatrix} U_{11}\\ U_{21}\\ \end{pmatrix} \Sigma_{1} \begin{pmatrix} V_{11}^{\intercal} & V_{21}^{\intercal} \end{pmatrix} + \begin{pmatrix} U_{12}\\ U_{22}\\ \end{pmatrix} \Sigma_{2} \begin{pmatrix} V_{12}^{\intercal} & V_{22}^{\intercal} \end{pmatrix}\\ &=\begin{pmatrix} U_{11}\Sigma_{1}V_{11}^{\intercal} & U_{11}\Sigma_{1}V_{21}^{\intercal}\\ U_{21}\Sigma_{1}V_{11}^{\intercal} & U_{21}\Sigma_{1}V_{21}^{\intercal}\\ \end{pmatrix} + \begin{pmatrix} U_{12}\Sigma_{2}V_{12}^{\intercal} & U_{12}\Sigma_{2}V_{22}^{\intercal}\\ U_{22}\Sigma_{2}V_{12}^{\intercal} & U_{22}\Sigma_{2}V_{22}^{\intercal}\\ \end{pmatrix} \\ & = U_{\bullet 1}\Sigma_1 V_{\bullet 1}^{\intercal} + U_{\bullet 2}\Sigma_2 V_{\bullet 2}^{\intercal}\\ & = A_{\max(r)} + A_{-\max(r)} \end{aligned}$$

其中，$U_{\bullet k}=[U_{1k}^{\intercal},U_{2k}^{\intercal}]^{\intercal},U_{k \bullet}=[U_{k1},U_{k2}]$。

已知秩$r$

$A_{\max(r)}$可视为矩阵$A$的秩$r$近似矩阵，显然$A_{\max(r)}$关于$\hat A_{22}$的Schur 补可表示为

$$U_{21}\Sigma_{1}V_{21}^{\intercal} = \{U_{21}\Sigma_{1}V_{11}^{\intercal}\} \{U_{11}\Sigma_{1}V_{11}^{\intercal}\}^{-1} \{U_{11}\Sigma_{1}V_{21}^{\intercal}\}$$

因此，可以使用$A_{\max(r)}$的分块矩阵$U_{21}\Sigma_{1}V_{21}^{\intercal}$部分来近似计算$A_{22}$。算法如下：

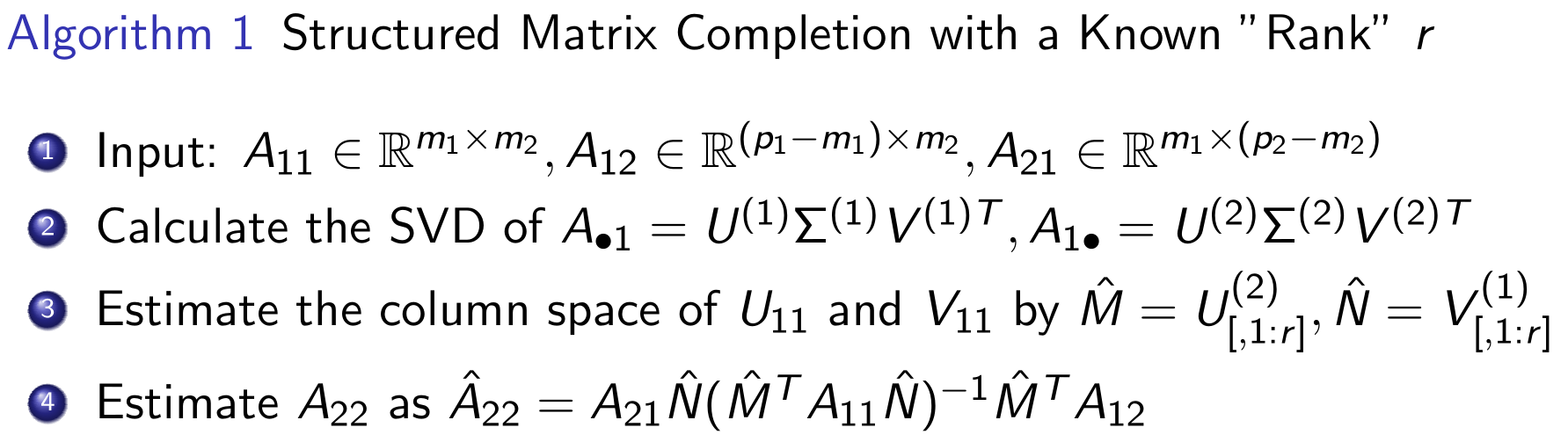
该算法存在以下限制：

• 需要已知秩$r$，这在实际应用中不可达。
• 需要计算矩阵除法（逆矩阵$(\hat M^T A_{11}\hat N)^{-1}$），当矩阵近似奇异或未知矩阵秩$r$时存在精度问题。

未知秩$r$

下面给出矩阵秩$r$的估计$\hat r$。

• 对$A_{1\bullet}$的列和$A_{\bullet 1}$的行进行旋转，将对$A_{1\bullet}$和$A_{\bullet 1}$的有意义的因子移至前面。

  • 对$A_{1\bullet}$和$A_{\bullet 1}$奇异值分解

    $$\begin{aligned} A_{\bullet 1} &= U^{(1)}\Sigma^{(1)} V^{(1)\intercal}\\ A_{1 \bullet} &= U^{(2)}\Sigma^{(2)}V^{(2)\intercal} \end{aligned}$$

  • 旋转后得到$Z_{11}, Z_{12}, Z_{21}$

    $$\begin{aligned} Z_{11} &= {U^{(2)}}^\intercal A_{11}V^{(1)}\\ Z_{12} &= {U^{(2)}}^\intercal A_{12} \\ Z_{21} &= A_{21}V^{(1)}\\ Z_{22} &= A_{22} \end{aligned}$$

• 若矩阵$A$的秩为$r$，则矩阵$Z$的第$r+1$行和第$r+1$列后面的元素都应该为0。一个秩$r$近似矩阵$A_{\max(r)}$的自然想法就是删除矩阵$Z$子块矩阵元素非常小的若干行若干列。

• 然而，当秩未知时，我们不清楚应该删除多少行多少列合适，因此可以尝试类似枚举法，一个一个试，保证

  • $Z_{11, [1:\hat r, 1:\hat r]}$非奇异
  • $\|Z_{21,[1:\hat r, 1:\hat r]}Z_{11,[1:\hat r, 1:\hat r]}^{-1}\| \leq T_R$，其中$T_R$是一个事先定义的标准
  • 找到满足上面两个要求的最大秩$\hat r$作为秩$r$的估计。

• 可用删除后的$Z_{21,[:, 1:\hat r]},Z_{11,[1:\hat r, 1:\hat r]},Z_{12[1:\hat r, :]}$来估计$A_{22}$

  $$\hat A_{22} = Z_{21,[:, 1:\hat r]}Z_{11, [1:\hat r, 1:\hat r]}^{-1}Z_{12, [1:\hat r, :]}$$

对应的算法如下：

注意：

• $Z_{21[:,1:r]}$和$Z_{11,[1:r,1:r]}$分别近似于$U_{21}\Sigma_1$和$\Sigma_1$
• 记$D_{R, s} = Z_{21, [:, 1:s]}Z_{11, [1:s, 1:s]}^{-1}$
• 用奇异性与范数估计秩：
  • 当$s > r$，$Z_{21[:,1:s]}$与$Z_{11,[1:s,1:s]}$近似奇异，因此$D_{R,s}$出现奇异或者无界的范数(singular or with unbounded norm)
  • 当$s = r$，$Z_{11, [1:s, 1:s]}$非奇异，则$\|D_{R, s}\|$有界

小结

• 该文章后面给出了两个算法的误差上、下界，补充文档给出详细的证明。

• 后续还会再找一些张老师的文章看看，算法简单易懂，理论就比较难懂了。🙇

• 文章还参考了一个外国友人做的slide^[3]，两个算法的截图来自于此。

References

---

1. Anru Zhang homepage: http://pages.stat.wisc.edu/~anruzhang/index.html (opens new window) ↩︎

2. Cai T , Cai T T , Zhang A . Structured Matrix Completion with Applications to Genomic Data Integration[J]. Journal of the American Statal Association, 2016, 111(514):621. ↩︎

3. slide: https://biostat.duke.edu/sites/biostat.duke.edu/files/Aaron Jones_Structured_Matrix_Completion.pdf (opens new window) ↩︎