写在前面

介绍最近看的基于$\ell_p$范数主成分分析(Principal Component Analysis, PCA)的文章^[1]

基于$\ell_p$范数的主成分分析

• $\ell_2$-PCA

$$F_2 (W) = \frac{1}{2}\sum_{i=1}^{N} \|W^T x_i\|_2^2 = \frac{1}{2} tr(W^T XX^T W)$$

• $\ell_1$-PCA

$$F_1 (W) = \sum_{i=1}^{N} \|W^T x_i\|_1 = \sum_{i=1}^{N} \sum_{j=1}^{m} |w_j^T x_i|$$

• $\ell_p$-PCA

$$F_p (W) = \frac{1}{p} \sum_{i=1}^{N} \|W^T x_i\|_p^p = \frac{1}{p} \sum_{i=1}^{N} \sum_{j=1}^{m} |w_j^T x_i|^p$$

求解算法($m=1$)

梯度下降

对应模型

$$w^* = \arg\min_w F_p(w) = \arg\min_w \frac{1}{p} \sum_{i=1}^{N} |w^T x_i|^p \quad \text{s.t.} w^Tw = 1$$

记$a_i = w^T x_i$，则 $F_p (w) = \frac{1}{p} \sum_{i=1}^{N} (\text{sgn}(a_i)a_i)^p$对$w$的梯度为

$$\begin{aligned} \nabla_{w} &=\frac{d F_{p}(w)}{d w}=\sum_{i=1}^{N} \frac{d F_{p}(w)}{d a_{i}} \frac{d a_{i}}{d w} \\ &=\sum_{i=1}^{N}\left[\text{sgn}\left(a_{i}\right) a_{i}\right]^{p-1}\left[\text{sgn}^{\prime}\left(a_{i}\right) a_{i}+\text{sgn}\left(a_{i}\right)\right] x_{i} \\ &=\sum_{i=1}^{N} \text{sgn}^{\prime}\left(a_{i}\right) \text{sgn}^{p-1}\left(a_{i}\right) a_{i}^{p} x_{i}+\sum_{i=1}^{N} \text{sgn}^{p}\left(a_{i}\right) a_{i}^{p-1} x_{i} \\ &=2 \sum_{i=1}^{N} \delta\left(a_{i}\right) \text{sgn}^{p-1}\left(a_{i}\right) a_{i}^{p} x_{i}+\sum_{i=1}^{N} \text{sgn}\left(a_{i}\right)\left|a_{i}\right|^{p-1} x_{i} \end{aligned}$$

当$a_i = w^T x_i \neq 0$，则梯度的第一项为0，即

$$\nabla_{w} = \sum_{i=1}^{N} \text{sgn}\left(w^T x_i\right)\left|w^T x_i\right|^{p-1} x_{i}$$

若$p > 1$，即使存在奇异点($w^T x_i = 0$)，第一项也为0，其梯度也是良定义的(见上式)。而当$p < 1$时需要对$w$进行扰动来避免奇异情况($w^T x_i = 0$)。

该问题可以通过最速下降法来迭代求解。

• 初值选取
  • $\ell_2$-PCA的结果
  • 具有最大范数的样本方向
• 学习率控制收敛速率，$\alpha = \frac{0.1}{N}$
• step 2 避免当$p \leq 1$时的奇异情况
• step 5 保证规范化$\|w\|_2 = 1$

基于梯度下降的PCA-Lp算法

梯度正交向量

$$\begin{aligned} \nabla_{w}^{\perp} &=\nabla_{w}-w\left(w^{T} \nabla_{w}\right)=\left(I_{d}-w w^{T}\right) \nabla_{w} \\ &=\left(I_{d}-w w^{T}\right) \sum_{i=1}^{N} \text{sgn}\left(w^{T} x_{i}\right)\left|w^{T} x_{i}\right|^{p-1} x_{i} \end{aligned}$$

令

$$c_i = \text{sgn}\left(w^{T} x_{i}\right)\left|w^{T} x_{i}\right|^{p-1}, v_i = \left(I_{d}-w w^{T}\right) x_{i}, f_i = c_i v_i$$

则

$$\nabla_{w}^{\perp} = \sum_{i=1}^{N} c_i v_i = \sum_{i=1}^{N} f_i$$

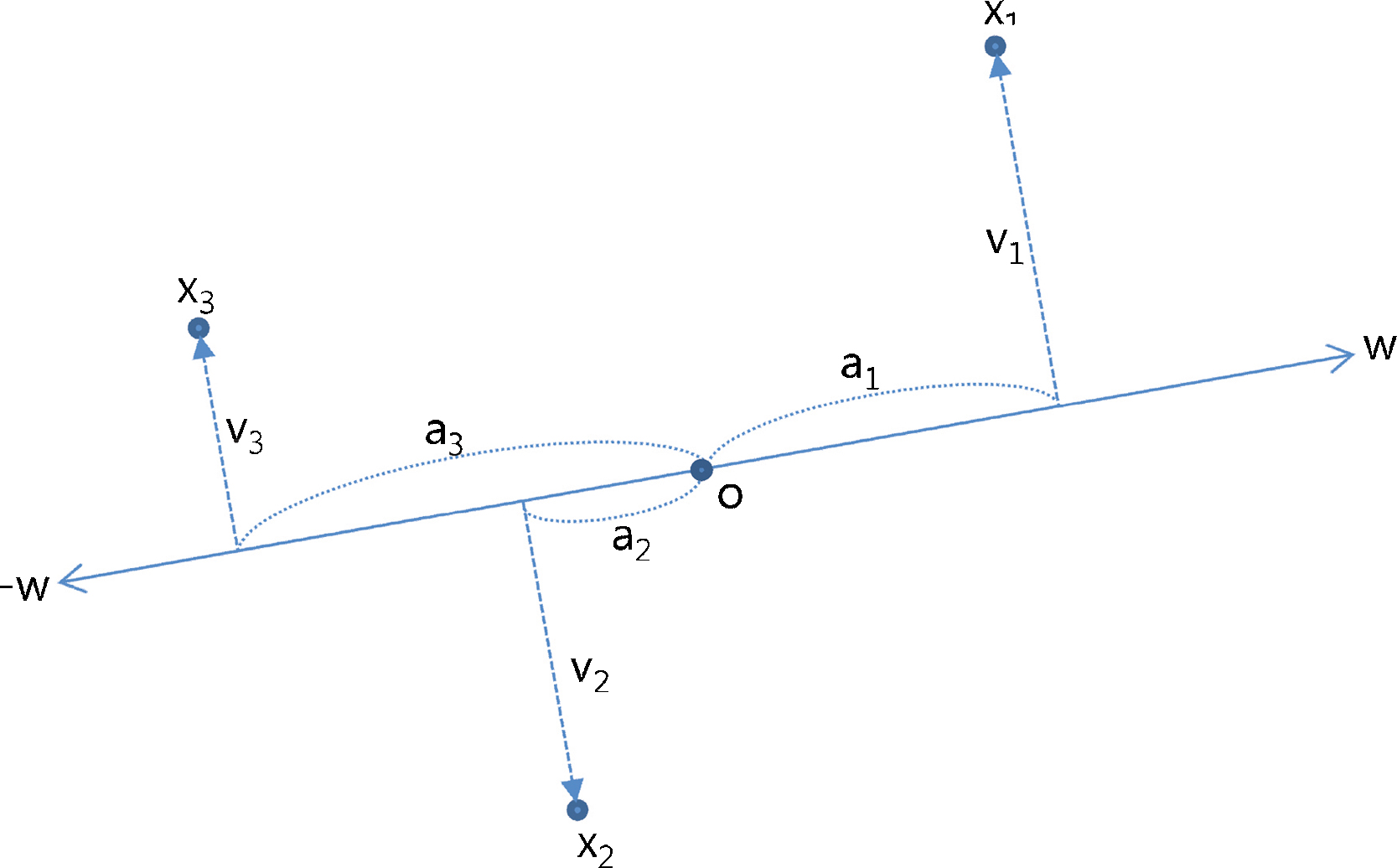
• $a_i = |w^T x_i|,v_i = x_i - w(w^T x_i)$
• $w$过原点$O$旋转
• 每一个样本 $x_i$ 对 $w$ 施加一个正交的力 $f_i$
  • 当 $w^T x_i > 0$ ，点 $x_i$ 对 $w$ 产生拉力
  • 当 $w^T x_i < 0$ ，点 $x_i$ 对 $w$ 产生推力，反之对 $-w$ 产生拉力
  • 力的大小为$|f_i| = a_i^{p-1}|v_i|$
    • $p=2$时，$|f_i| = a_i|v_i|$，力收到两方面的乘积影响(拟合性)
    • $p=1$时，$|f_i| = |v_i|$，力只收到一方面的乘积影响(鲁棒性)
    • $p<1$时，$|f_i| = (\frac{|v_i|}{a_i})^{1-p}|v_i|^p$，$a_i$对力产生负影响，从而降低异常值的干扰
    • $p \to 0$时，$|f_i| = \frac{|v_i|}{a_i}$

传统PCA联系

当$p = 2$时

$$\nabla_{w} = \sum_{i=1}^{N} \text{sgn}\left(w^T x_i\right)\left|w^T x_i\right|^{p-1} x_{i} = \sum_{i=1}^{N} x_{i} x_i^T w$$

$$\nabla_{w}^{\perp} =\left(I_{d}-w w^{T}\right) \sum_{i=1}^{N} \text{sgn}\left(w^{T} x_{i}\right)\left|w^{T} x_{i}\right|^{p-1} x_{i} = \left(I_{d}-w w^{T}\right) XX^T w$$

因此优化问题可以通过协方差矩阵的特征值分解解决。而梯度正交向量有如下性质：

$$\nabla_{w}^{\perp} = 0 \iff \nabla_{w} = XX^T w$$

拉格朗日乘子法

约束优化问题转化为如下

$$L(w, \lambda ) = F_p(w) + \lambda (w^T w - 1)$$

令拉格朗日函数导数为0可得最优解的必要性

$$\frac{dL(w,\lambda)}{dw} = \nabla_w + \lambda w = 0$$

可得$w$与梯度$\nabla_w$平行，又$\|w\|_2=1$，因此可对$w$直接更新

$$w \leftarrow \frac{\nabla_w}{\|\nabla_w\|_2}$$

通常情况下，这种令导数为零方法取到的不仅是最大值，也有可能是最小值。因此在$\ell_p$-PCA里，对$p \geq 1$，由$F_p$的凸性可得该迭代下的目标函数非减。

$$F_p(w^{k+1}) \geq F_p(w^{k}) + \nabla_w^T (w^{k+1} - w^{k}) \geq F_p(w^{k})$$

第二个不等号是因为$\|w^{k+1}\|_2 = \|w^{k}\|_2 = 1$且$w^{k+1}$平行于$\nabla_w$，$\nabla_w^T w^{k+1} = 1$。

基于Lagrangian乘子法的PCA-Lp算法

求解算法($m>1$)

贪婪算法（近似求解）

• 往往求得局部最优解，而不是全局最优解

非贪婪解

对目标函数求梯度

$$\nabla_W = \frac{dF_p(W)}{dW} = [\nabla_{w_1},\dots,\nabla_{w_m}]$$

对应的拉格朗日函数为

$$L(W, \Gamma_m ) = F_p(W) + tr(\Gamma_m^T (W^T W - I_m))$$

同样的，设导数为0，即

$$\frac{dL(W, \Gamma_m )}{dW} = \nabla_W + 2W\Gamma_m = 0$$

迭代不能再是简单的赋值，需满足正交约束，因此考虑如下优化问题

$$W^* = \arg\max_Q tr(Q^T \nabla_W) \quad \text{s.t.} Q^T Q = I_m$$

设$\nabla_W$的SVD分解为$\nabla_W = U\Lambda V^T$，记$Z = V^T Q^T U$，得$ZZ^T = I_d,z_{ii}\leq 1$。因此

$$\begin{aligned} tr(Q^T \nabla_W) &= tr(Q^T U\Lambda V^T) = tr(\Lambda V^T Q^T U) \\ &= tr(\Lambda Z) = \sum_i \lambda_{ii}z_{ii} \leq \sum_i \lambda_{ii} \end{aligned}$$

取等号时当且仅当$z_{ii} = 1$，此时$Z = [I_m | 0]$，最优解

$$W^* = U Z^T V^T = U [I_m | 0]^T V^T$$

参考文献

---

1. Kwak N. Principal component analysis by Lp-norm maximization. IEEE Trans Cybern. 2014;44(5):594-609. ↩︎